Leetcode Day 42 - Monotone stack Advanced

Monotone stack

Diff	Problem	Python	Java
	42 Trapping Rain Water	✅
	84 Largest Rectangle in Histogram	✅

Trapping Rain Water

Link to Leetcode question¹

Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it can trap after raining.

Example 1

Input: height = [0,1,0,2,1,0,1,3,2,1,2,1]
Output: 6
Explanation: The above elevation map (black section) is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped.

Example 2

Input: height = [4,2,0,3,2,5]
Output: 9

Solution

A detailed explaination of solution can be found here².

Double Pointers

class Solution(object):
    def trap(self, height):
        h = len(height)
        max_left = [0] * h
        max_left[0] = height[0]
        max_right = [0] * h
        max_right[-1] = height[-1]

        for i in range(1,h):
            max_left[i] = max(height[i], max_left[i - 1])
            
        for j in range(h - 2, -1, -1):
            max_right[j] = max(height[j], max_right[j + 1])
        
        water = 0

        for num in range(1, h - 1):
            water += max(min(max_left[num - 1], max_right[num + 1]) - height[num], 0)
        
        return water

class Solution(object):
    def trap(self, height):
        left = 0
        right = len(height) - 1
        left_max = height[0]
        right_max = height[len(height) - 1]
        water = 0
        
        while left < right:
            if left_max < right_max:
                left += 1
                if left_max < height[left]:
                    left_max = height[left]
                else:
                    water += left_max - height[left]
            else:
                right -= 1
                if right_max < height[right]:
                    right_max = height[right]
                else:
                    water += right_max - height[right]
        
        return water

Monotone stack

class Solution(object):
    def trap(self, height):
        stack = [0]
        water = 0

        for i in range(1, len(height)):
            if height[i] < height[stack[-1]]:
                stack.append(i)
            elif height[i] == height[stack[-1]]:
                stack[-1] = i
            else:
                while len(stack) > 0 and height[i] > height[stack[-1]]:
                    if len(stack) > 1:
                        water += (i - stack[-2] - 1) * (min(height[i], height[stack[-2]]) - height[stack[-1]])
                    stack.pop()
                
                stack.append(i)
        
        return water

Largest Rectangle in Histogram

Link to Leetcode question³

Given an array of integers heights representing the histogram’s bar height where the width of each bar is 1, return the area of the largest rectangle in the histogram.

Example 1

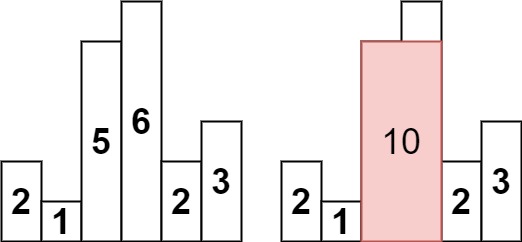
Input: heights = [2,1,5,6,2,3]
Output: 10
Explanation: The above is a histogram where width of each bar is 1.
The largest rectangle is shown in the red area, which has an area = 10 units.

Example 2

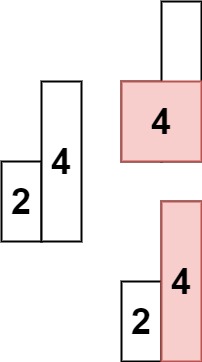
Input: heights = [2,4]
Output: 4

Solution

A detailed explaination of solution can be found here⁴.

Python

class Solution:
    def largestRectangleArea(self, heights):
        if not heights:
            return 0
        
        max_area = 0
        stack = []
        n = len(heights)

        for i in range(n + 1):
            while stack and (i == n or heights[i] < heights[stack[-1]]):
                h = heights[stack.pop()]
                w = i if not stack else i - stack[-1] - 1
                max_area = max(max_area, h * w)
            stack.append(i)
        
        return max_area

Reference

1. Leetcode-42 Trapping Rain Water: https://leetcode.com/problems/trapping-rain-water/description/. ↩︎

2. 代码随想录-接雨水: https://programmercarl.com/0042.接雨水.html. ↩︎

3. Leetcode-84 Largest Rectangle in Histogram: https://leetcode.com/problems/largest-rectangle-in-histogram/description/. ↩︎

4. 代码随想录-柱状图中最大的矩形: https://programmercarl.com/0084.柱状图中最大的矩形.html. ↩︎