Post

Leetcode Day 38 - DP: Subsequence

1143 Longest Common Subsequence | 1035 Uncrossed Lines | 53 Maximum Subarray | 392 Is Subsequence

Posted
By Le Lyu
views 6 min read

Dynamic Programming

DiffProblemPythonJava
Medium1143 Longest Common Subsequence✅ 
Medium1035 Uncrossed Lines✅ 
Easy53 Maximum Subarray✅ 
Easy392 Is Subsequence✅ 

Longest Common Subsequence

Link to Leetcode question1

Given two strings text1 and text2, return the length of their longest common subsequence. If there is no common subsequence, return 0.

A subsequence of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.

For example, "ace" is a subsequence of "abcde". A common subsequence of two strings is a subsequence that is common to both strings.

Example 1

1
2
3

Input: text1 = "abcde", text2 = "ace" 
Output: 3  
Explanation: The longest common subsequence is "ace" and its length is 3.

Example 2

1
2
3

Input: text1 = "abc", text2 = "abc"
Output: 3
Explanation: The longest common subsequence is "abc" and its length is 3.

Example 3

1
2
3

Input: text1 = "abc", text2 = "def"
Output: 0
Explanation: There is no such common subsequence, so the result is 0.

Solution

A detailed explaination of solution can be found here[^lcsSolution].

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution(object):
    def longestCommonSubsequence(self, text1, text2):
        text1, text2 = list(text1), list(text2)
        n1 = len(text1)
        n2 = len(text2)

        dp = [[0] * (n2 + 1) for _ in range(n1 + 1)]
        result = 0

        for t1 in range(1,n1 + 1):
            for t2 in range(1,n2 + 1):
                temp = max(dp[t1][t2 - 1], dp[t1 - 1][t2])
                if dp[t1 - 1][t2 - 1] < temp: 
                    dp[t1][t2] = temp
                else:
                    dp[t1][t2] = dp[t1 - 1][t2 - 1]
                    if text1[t1 - 1] == text2[t2 - 1]:
                        dp[t1][t2] += 1
                        if dp[t1][t2] > result: result = dp[t1][t2]

        return result

Use scrolling arrays to increase efficiency

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class Solution(object):
    def longestCommonSubsequence(self, text1, text2):
        n1, n2 = len(text1), len(text2)
        
        # 确保使用较短的字符串进行列计算，以节省空间
        if n1 < n2:
            text1, text2 = text2, text1
            n1, n2 = n2, n1
        
        # 滚动数组优化空间，只保留前一行和当前行
        prev = [0] * (n2 + 1)
        curr = [0] * (n2 + 1)
        
        for i in range(1, n1 + 1):
            for j in range(1, n2 + 1):
                if text1[i - 1] == text2[j - 1]:
                    curr[j] = prev[j - 1] + 1
                else:
                    curr[j] = max(prev[j], curr[j - 1])
            # 交换 prev 和 curr
            prev, curr = curr, prev
        
        # 结果在最后一行
        return prev[n2]

Uncrossed Lines

Link to Leetcode question[^ul]

You are given two integer arrays nums1 and nums2. We write the integers of nums1 and nums2 (in the order they are given) on two separate horizontal lines.

We may draw connecting lines: a straight line connecting two numbers nums1[i] and nums2[j] such that:

  • nums1[i] == nums2[j], and
  • the line we draw does not intersect any other connecting (non-horizontal) line.

Note that a connecting line cannot intersect even at the endpoints (i.e., each number can only belong to one connecting line).

Return the maximum number of connecting lines we can draw in this way.

Example 1

Desktop View

1
2
3
4

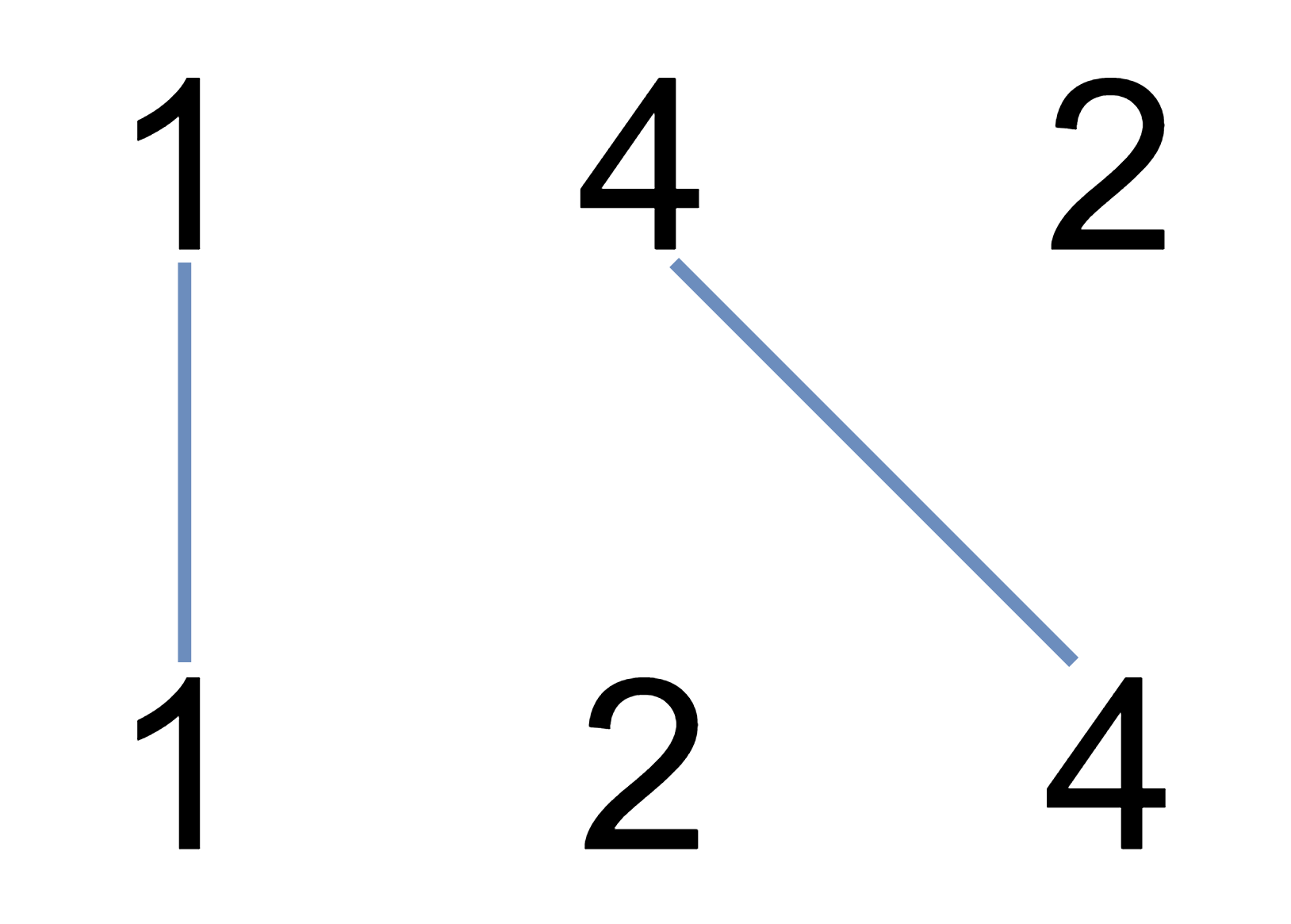
Input: nums1 = [1,4,2], nums2 = [1,2,4]
Output: 2
Explanation: We can draw 2 uncrossed lines as in the diagram.
We cannot draw 3 uncrossed lines, because the line from nums1[1] = 4 to nums2[2] = 4 will intersect the line from nums1[2]=2 to nums2[1]=2.

Example 2

1
2

Input: nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]
Output: 3

Example 3

1
2

Input: nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1]
Output: 2

Solution

A detailed explaination of solution can be found here[^ulSolution].

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

class Solution(object):
    def maxUncrossedLines(self, nums1, nums2):
        n1, n2 = len(nums1), len(nums2)
        
        if n1 < n2:
            nums1, nums2 = nums2, nums1
            n1, n2 = n2, n1
        
        prev = [0] * (n2 + 1)
        curr = [0] * (n2 + 1)
        
        for i in range(1, n1 + 1):
            for j in range(1, n2 + 1):
                if nums1[i - 1] == nums2[j - 1]:
                    curr[j] = prev[j - 1] + 1
                else:
                    curr[j] = max(prev[j], curr[j - 1])
            prev, curr = curr, prev
        
        return prev[n2]

Maximum Subarray

Link to Leetcode question[^ms]

Given an integer array nums, find the subarray with the largest sum, and return its sum.

Example 1

1
2
3

Input: nums = [-2,1,-3,4,-1,2,1,-5,4]
Output: 6
Explanation: The subarray [4,-1,2,1] has the largest sum 6.

Example 2

1
2
3

Input: nums = [1]
Output: 1
Explanation: The subarray [1] has the largest sum 1.

Example 3

1
2
3

Input: nums = [5,4,-1,7,8]
Output: 23
Explanation: The subarray [5,4,-1,7,8] has the largest sum 23.

Solution

A detailed explaination of solution can be found here[^msSolution]. A detailed explaination of greedy solution can be found here.

Python

1
2
3
4
5
6
7
8
9
10

class Solution:
    def maxSubArray(self, nums):
        cur_num = nums[0]
        result =  cur_num

        for i in range(1, len(nums)):
            cur_num = max(cur_num + nums[i], nums[i])
            if cur_num > result: result = cur_num
        
        return result

Is Subsequence

Link to Leetcode question[^is]

Given two strings s and t, return true if s is a subsequence of t, or false otherwise.

A subsequence of a string is a new string that is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (i.e., "ace" is a subsequence of "abcde" while "aec" is not).

Example 1

1
2

Input: s = "abc", t = "ahbgdc"
Output: true

Example 2

1
2

Input: s = "axc", t = "ahbgdc"
Output: false

Solution

A detailed explaination of solution can be found here[^isSolution].

Python

1
2
3
4
5
6
7
8
9
10
11
12
13

class Solution(object):
    def isSubsequence(self, s, t):
        ls = len(s)
        if ls == 0: return True
        
        target = 0

        for j in range(len(t)):
            if t[j] == s[target]:
                target += 1
                if target == ls: return True

        return False

Reference

](https://leetcode.com/problems/longest-common-subsequence/description/). [^lcsSolution]:代码随想录-最长公共子序列: https://programmercarl.com/1143.最长公共子序列.html. [^ul]:Leetcode-1035 Uncrossed Lines: https://leetcode.com/problems/uncrossed-lines/description/. [^ulSolution]:代码随想录-不相交的线: https://programmercarl.com/1035.不相交的线.html. [^ms]:Leetcode-53 Maximum Subarray: https://leetcode.com/problems/maximum-subarray/description/. [^msSolution]:代码随想录-最大子序和: https://programmercarl.com/0053.最大子序和（动态规划）.html. [^is]:Leetcode-392 Is Subsequence: https://leetcode.com/problems/is-subsequence/description/. [^isSolution]:代码随想录- https://programmercarl.com/0392.判断子序列.html.

  1. Leetcode-1143 Longest Common Subsequence: [https://leetcode.com/problems/longest-common-subsequence/description/ ↩︎

Data Structure and Algorithm, Leetcode, Dynamic Programming
dynamic programming (DP)
This post is licensed under CC BY 4.0 by the author.