Leetcode Day 29 - Dynamic Programming

Dynamic Programming

Link to note about Dynamic Programming

Diff	Problem	Python	Java
	62 Unique Paths	✅
	63 Unique Paths II	✅
	343 Integer Break	✅
	96 Unique Binary Search Trees	✅

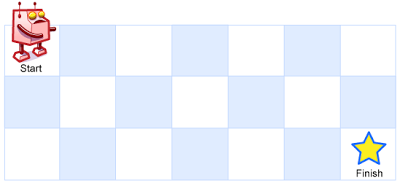
Unique Paths

Link to Leetcode question¹

here is a robot on an m x n grid. The robot is initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m - 1][n - 1]). The robot can only move either down or right at any point in time.

Given the two integers m and n, return the number of possible unique paths that the robot can take to reach the bottom-right corner.

The test cases are generated so that the answer will be less than or equal to 2 * 109.

Example 1

Input: m = 3, n = 7
Output: 28

*Example 2**

Input: m = 3, n = 2
Output: 3
Explanation: From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:

1. Right -> Down -> Down
   
2. Down -> Down -> Right
   
3. Down -> Right -> Down
   

Solution

A detailed explaination of solution can be found here².

Python

class Solution(object):
    def uniquePaths(self, m, n):
        if m == 1 or n == 1:
            return 1
        
        grid = [[0] * n for _ in range(m)]
        grid[0][0] = 1

        for M in range(m):
            for N in range(n):
                if M != 0: grid[M][N] += grid[M - 1][N]
                if N != 0: grid[M][N] += grid[M][N - 1]

        return grid[-1][-1]

Unique Paths II

Link to Leetcode question³

You are given an m x n integer array grid. There is a robot initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m - 1][n - 1]). The robot can only move either down or right at any point in time.

An obstacle and space are marked as 1 or 0 respectively in grid. A path that the robot takes cannot include any square that is an obstacle.

Return the number of possible unique paths that the robot can take to reach the bottom-right corner.

The testcases are generated so that the answer will be less than or equal to 2 * 109.

Example 1

Input: obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
Output: 2
Explanation: There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:

1. Right -> Right -> Down -> Down
   
2. Down -> Down -> Right -> Right

Input: obstacleGrid = [[0,1],[0,0]]
Output: 1

Solution

A detailed explaination of solution can be found here⁴.

Python

class Solution(object):
    def uniquePathsWithObstacles(self, obstacleGrid):
        if obstacleGrid[0][0] == 1 or obstacleGrid[-1][-1] == 1: return 0
        m, n = len(obstacleGrid), len(obstacleGrid[0])
        
        grid = [[0] * n for _ in range(m)]
        grid[0][0] = 1

        for M in range(m):
            for N in range(n):
                if obstacleGrid[M][N] == 1: continue
                if M != 0: grid[M][N] += grid[M - 1][N]
                if N != 0: grid[M][N] += grid[M][N - 1]

        return grid[-1][-1]

Similar Questions

Diff	Similar Questions	Python	Java
	64 Minimum Path Sum5
	2304 Minimum Path Cost in a Grid6
	980 Unique Paths III7

Integer Break

Link to Leetcode question⁸

Given an integer n, break it into the sum of k positive integers, where k >= 2, and maximize the product of those integers.

Return the maximum product you can get.

Example 1

Input: n = 2
Output: 1
Explanation: 2 = 1 + 1, 1 × 1 = 1.

Example 2

Input: n = 10
Output: 36
Explanation: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36.

Solution

A detailed explaination of solution can be found here⁹.

Solution 1: Dynamic Programming

Time complexity: O(n²)

class Solution(object):
    def integerBreak(self, n):
        if n == 2: return 1
        if n == 3: return 2

        dp = [0] * (n + 1)
        dp[2], dp[3] = 2, 3

        for i in range(4, n+1):
            for j in range(1, i // 2 + 1):
                dp[i] = max(dp[i], dp[j] * dp[i - j])
        
        return dp[n]

Solution 2: Greedy

Time complexity: O(1)

The second solution uses a greedy algorithm. It directly breaks down n into as many 3’s as possible, aiming to maximize the product of the integer breakdown. This approach is based on a mathematical pattern, and it returns the maximum product directly by considering different cases.

By breaking down n, we can observe that the more we break n into 3’s, the larger the product becomes. However, there are two special cases to consider:

• When n % 3 == 1: Splitting out a 4 is better than splitting out a 1 (i.e., 3 * 3 * 1 < 3 * 4).
• When n % 3 == 2: Directly multiplying by 2 yields the optimal product.

1. If n is a multiple of 3: We can completely break n into 3’s, and the maximum product is 3 ** (n // 3).
2. If n % 3 == 1: Since the remainder 1 would decrease the product, we adjust by removing one 3 and replacing it with 4 (because 3 + 1 = 4). The maximum product in this case is 3 ** ((n // 3) - 1) * 4.
3. If n % 3 == 2: The remainder 2 can be directly multiplied, so the maximum product is 3 ** (n // 3) * 2.

class Solution(object):
    def integerBreak(self, n):
        if n == 2: return 1
        if n == 3: return 2
        if n % 3 == 0: return 3 ** (n // 3)
        if n % 3 == 1: return 3 ** ((n // 3) - 1) * 4
        return 3 ** (n // 3) * 2


```python
class Solution(object):
    def integerBreak(self, n):
        if n == 2: return 1
        if n == 3: return 2
        if n % 3 == 0: return 3 ** (n // 3)
        if n % 3 == 1: return 3 ** ((n // 3) - 1) * 4
        return 3 ** (n // 3) * 2

Similar Questions

Diff	Similar Questions	Python	Java
	1808 Maximize Number of Nice Divisors10

Unique Binary Search Trees

Link to Leetcode question¹¹

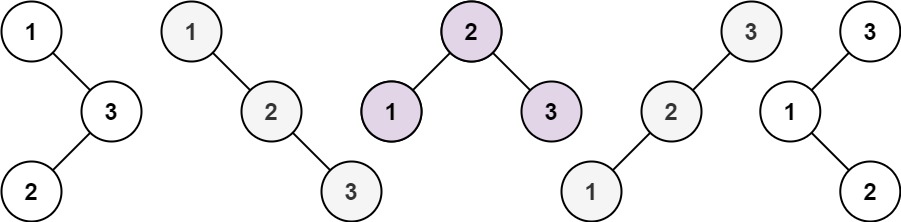
Given an integer n, return the number of structurally unique BST’s (binary search trees) which has exactly n nodes of unique values from 1 to n.

Example 1

Input: n = 3
Output: 5

Example 2

Input: n = 1
Output: 1

Solution

A detailed explaination of solution can be found here¹².

Python

class Solution(object):
    def numTrees(self, n):
        if n == 1: return 1
        if n == 2: return 2

        dp = [0] * (n + 1)
        dp[0],dp[1], dp[2] = 1, 1, 2
        

        for i in range(3,n + 1):
            for j in range((i - 1) // 2 + 1):
                dp[i] += dp[j] * dp[i - j - 1] * 2 if j != i - j - 1 else dp[j] * dp[i - j - 1]
        
        return dp[n]

Similar Questions

Diff	Similar Questions	Python	Java
	95 Unique Binary Search Trees II13

Reference

1. Leetcode-62 Unique Paths: https://leetcode.com/problems/unique-paths/description/. ↩︎

2. 代码随想录-不同路径: https://programmercarl.com/0062.不同路径.html. ↩︎

3. Leetcode-63 Unique Paths II: https://leetcode.com/problems/unique-paths-ii/description/. ↩︎

4. 代码随想录-不同路径II: https://programmercarl.com/0063.不同路径II.html. ↩︎

5. Leetcode-64 Minimum Path Sum: https://leetcode.com/problems/minimum-path-sum/description/. ↩︎

6. Leetcode-2304 Minimum Path Cost in a Grid: https://leetcode.com/problems/minimum-path-cost-in-a-grid/description/. ↩︎

7. Leetcode-980 Unique Paths III: https://leetcode.com/problems/unique-paths-iii/. ↩︎

8. Leetcode-343 Integer Break: https://leetcode.com/problems/integer-break/description/. ↩︎

9. 代码随想录-整数拆分: https://programmercarl.com/0343.整数拆分.html. ↩︎

10. Leetcode-1808 Maximize Number of Nice Divisors: https://leetcode.com/problems/maximize-number-of-nice-divisors/. ↩︎

11. Leetcode-96 Unique Binary Search Trees: https://leetcode.com/problems/unique-binary-search-trees/description/. ↩︎

12. 代码随想录-不同的二叉搜索树: https://programmercarl.com/0096.不同的二叉搜索树.html. ↩︎

13. Leetcode-95 Unique Binary Search Trees II: https://leetcode.com/problems/unique-binary-search-trees-ii/description/. ↩︎