Post

Leetcode Day 17 - Binary Search Tree: Insertion, Deletion, and LCA

Focuses on essential binary search tree (BST) operations, including finding the lowest common ancestor, inserting new nodes, and deleting nodes from a BST while maintaining its properties.

Posted Updated
By Le Lyu
views 6 min read

Binary Tree

Link to note about binary tree

DiffProblemPythonJava
Medium235 Lowest Common Ancestor of a Binary Search Tree✅ 
Medium701 Insert into a Binary Search Tree✅ 
Medium450 Delete Node in a BST✅ 

Lowest Common Ancestor of a Binary Search Tree

Link to Leetcode question1

Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Example 1

Desktop View

1
2
3

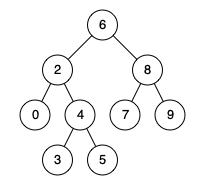
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.

Example 2

Desktop View

1
2
3

Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.

Example 3

1
2

Input: root = [2,1], p = 2, q = 1
Output: 2

Solution

A detailed explaination of solution can be found here2.

Python

1
2
3
4
5
6
7
8
9
10
11
12
13

class Solution(object):
    def lowestCommonAncestor(self, root, p, q):
        if root is None:
            return None
        
        if (p.val <= root.val and q.val >= root.val) or (p.val >= root.val and q.val <= root.val):
            return root
        
        if p.val <= root.val and q.val <= root.val:
            return self.lowestCommonAncestor(root.left, p, q)
        
        if p.val >= root.val and q.val >= root.val:
            return self.lowestCommonAncestor(root.right, p, q)

Insert into a Binary Search Tree

Link to Leetcode question3

You are given the root node of a binary search tree (BST) and a value to insert into the tree. Return the root node of the BST after the insertion. It is guaranteed that the new value does not exist in the original BST.

Notice that there may exist multiple valid ways for the insertion, as long as the tree remains a BST after insertion. You can return any of them.

Example 1

Desktop View

1
2
3

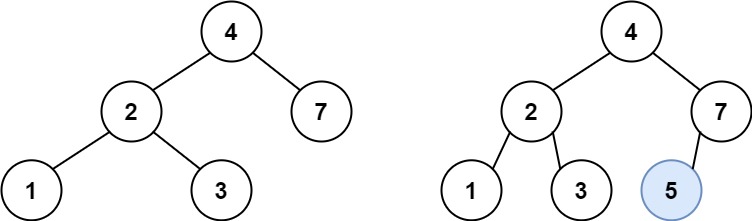
Input: root = [4,2,7,1,3], val = 5
Output: [4,2,7,1,3,5]
Explanation: Another accepted tree is:

Desktop View

Example 2

1
2

Input: root = [40,20,60,10,30,50,70], val = 25
Output: [40,20,60,10,30,50,70,null,null,25]

Example 3

1
2

Input: root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
Output: [4,2,7,1,3,5]

Solution

A detailed explaination of solution can be found here4.

Python

1
2
3
4
5
6
7
8
9
10
11

class Solution(object):
    def insertIntoBST(self, root, val):
        if root is None:
            return TreeNode(val)
        
        if val < root.val:
            root.left = self.insertIntoBST(root.left, val)
            return root
        
        root.right = self.insertIntoBST(root.right, val)
        return root

Delete Node in a BST

Link to Leetcode question5

Given a root node reference of a BST and a key, delete the node with the given key in the BST. Return the root node reference (possibly updated) of the BST.

Basically, the deletion can be divided into two stages:

  1. Search for a node to remove.
  2. If the node is found, delete the node.

Example 1

Desktop View

1
2
3
4
5

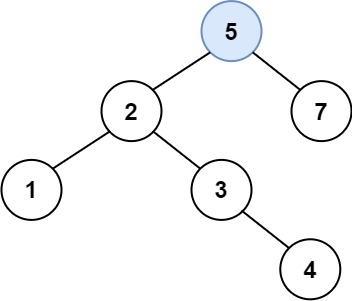
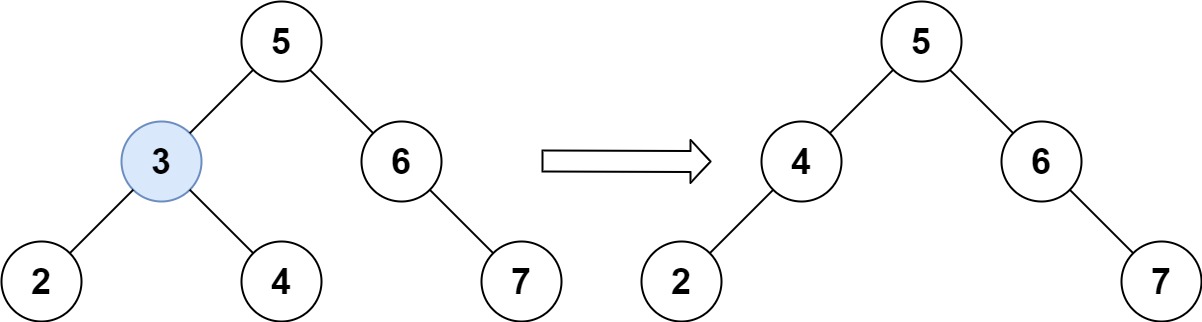
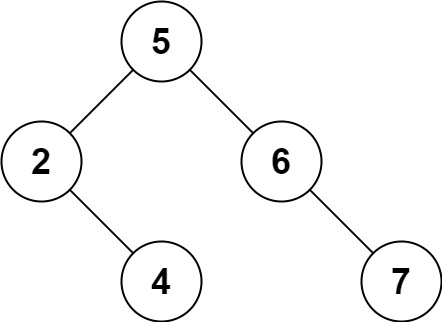
Input: root = [5,3,6,2,4,null,7], key = 3
Output: [5,4,6,2,null,null,7]
Explanation: Given key to delete is 3. So we find the node with value 3 and delete it.
One valid answer is [5,4,6,2,null,null,7], shown in the above BST.
Please notice that another valid answer is [5,2,6,null,4,null,7] and it's also accepted.

Desktop View

Example 2

1
2
3

Input: root = [5,3,6,2,4,null,7], key = 0
Output: [5,3,6,2,4,null,7]
Explanation: The tree does not contain a node with value = 0.

Example 3

1
2

Input: root = [], key = 0
Output: []

Solution

A detailed explaination of solution can be found here6.

The deletion process involves handling three distinct cases once the node to be deleted is located.

**Case **1: Node is a Leaf (No Child Nodes)

If the node has no left or right child, we simply delete this node by returning None. T

1
2

if not root.left and not root.right:
    return None

Case 2: Node has One Child

If the node to be deleted has only one child, we replace the node with its single child. This is done by returning the child node, which will take the place of the deleted node.

  • Left Child Only: If the node has only a left child, return the left child.
  • Right Child Only: If the node has only a right child, return the right child.
1
2
3
4

if not root.left:
    return root.right
elif not root.right:
    return root.left

Case 3: Node has Two Children

If the node has two children, this is the most complex case. To maintain the BST properties, we need to:

  1. Find the smallest node in the right subtree (in-order successor). This node is guaranteed to be larger than all nodes in the left subtree and smaller than all other nodes in the right subtree.
1

  min_larger_node = self.findMin(root.right)
  1. Replace the value of the node to be deleted with the value of the in-order successor. This ensures that the BST property remains intact.
1

  root.val = min_larger_node.val

  1. Recursively delete the in-order successor from the right subtree since its value has been moved to the current node. This step ensures that the tree does not contain duplicate values.

    1

    root.right = self.deleteNode(root.right, min_larger_node.val)

Complete Code

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class Solution(object):
    def deleteNode(self, root, key):
        if not root:
            return None
        
        if key < root.val:
            root.left = self.deleteNode(root.left, key)
        elif key > root.val:
            root.right = self.deleteNode(root.right, key)
        else:
            if not root.left:
                return root.right
            elif not root.right:
                return root.left
            
            min_larger_node = self.findMin(root.right)
            root.val = min_larger_node.val
            root.right = self.deleteNode(root.right, min_larger_node.val)
        return root
    
    def findMin(self, node):
        while node.left:
            node = node.left
        return node

Reference

  1. Leetcode-235 Lowest Common Ancestor of a Binary Search Tree: https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-search-tree/description/. ↩︎

  2. 代码随想录-二叉搜索树的最近公共祖先: https://programmercarl.com/0235.二叉搜索树的最近公共祖先.html#算法公开课. ↩︎

  3. Leetcode-701 Insert into a Binary Search Tree: https://leetcode.com/problems/insert-into-a-binary-search-tree/description/. ↩︎

  4. 代码随想录-二叉搜索树中的插入操作: https://programmercarl.com/0701.二叉搜索树中的插入操作.html. ↩︎

  5. Leetcode-450 Delete Node in a BST: https://leetcode.com/problems/delete-node-in-a-bst/description/. ↩︎

  6. 代码随想录-删除二叉搜索树中的节点: https://programmercarl.com/0450.删除二叉搜索树中的节点.html. ↩︎

Data Structure and Algorithm, Leetcode, Binary Tree
binary tree
This post is licensed under CC BY 4.0 by the author.