Leetcode Day 15 - Binary Tree: Construction and Search Operations

Binary Tree

Link to note about binary tree

Diff	Problem	Python	Java
	654 Maximum Binary Tree	✅
	617 Merge Two Binary Trees	✅
	700 Search in a Binary Search Tree	✅
	98 Validate Binary Search Tree	✅

Maximum Binary Tree

Link to Leetcode question¹

You are given an integer array nums with no duplicates. A maximum binary tree can be built recursively from nums using the following algorithm:

• Create a root node whose value is the maximum value in nums.
• Recursively build the left subtree on the subarray prefix to the left of the maximum value.
• Recursively build the right subtree on the subarray suffix to the right of the maximum value.
• Return the maximum binary tree built from nums.

Example 1

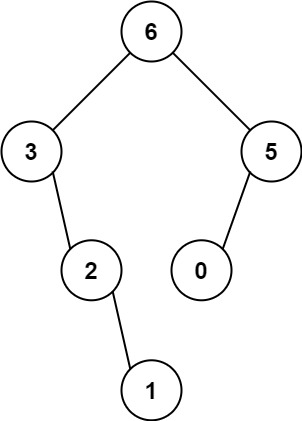
Input: nums = [3,2,1,6,0,5]
Output: [6,3,5,null,2,0,null,null,1]

Explanation: The recursive calls are as follow:

• The largest value in [3,2,1,6,0,5] is 6. Left prefix is [3,2,1] and right suffix is [0,5].
  • The largest value in [3,2,1] is 3. Left prefix is [] and right suffix is [2,1].
    • Empty array, so no child.
    • The largest value in [2,1] is 2. Left prefix is [] and right suffix is [1].
      • Empty array, so no child.
      • Only one element, so child is a node with value 1.
  • The largest value in [0,5] is 5. Left prefix is [0] and right suffix is [].
    • Only one element, so child is a node with value 0.
    • Empty array, so no child.

Example 2

Input: nums = [3,2,1]
Output: [3,null,2,null,1]

Solution

A detailed explaination of solution can be found here².

Python

class Solution(object):
    def constructMaximumBinaryTree(self, nums):
        if len(nums) == 1:
            return TreeNode(val = nums[0])
        
        max_index, max_value = 0, nums[0]
        for i in range(len(nums)):
            if nums[i] > max_value:
                max_index = i
                max_value = nums[i]
        
        node = TreeNode(max_value)
        if max_index > 0:
            node.left = self.constructMaximumBinaryTree(nums[:max_index])
        if max_index < len(nums) - 1:
            node.right = self.constructMaximumBinaryTree(nums[max_index + 1:])
        
        return node

Similar Questions

Diff	Similar Questions	Python	Java
	998 Maximum Binary Tree II3

Merge Two Binary Trees

Link to Leetcode question⁴

You are given two binary trees root1 and root2.

Imagine that when you put one of them to cover the other, some nodes of the two trees are overlapped while the others are not. You need to merge the two trees into a new binary tree. The merge rule is that if two nodes overlap, then sum node values up as the new value of the merged node. Otherwise, the NOT null node will be used as the node of the new tree.

Return the merged tree.

Note: The merging process must start from the root nodes of both trees.

Example 1

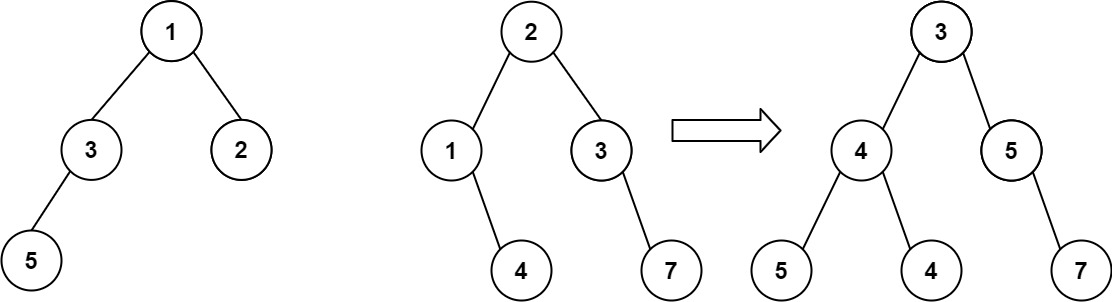
Input: root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
Output: [3,4,5,5,4,null,7]

Example 2

Input: root1 = [1], root2 = [1,2]
Output: [2,2]

Solution

A detailed explaination of solution can be found here⁵.

Python

class Solution(object):
    def mergeTrees(self, root1, root2):
        if root1 is None and root2 is None:
            return None
        if root1 is None:
            return root2
        if root2 is None:
            return root1
        
        node = TreeNode(root1.val + root2.val)

        node.left = self.mergeTrees(root1.left, root2.left)
        node.right = self.mergeTrees(root1.right, root2.right)

        return node

Search in a Binary Search Tree

Link to Leetcode question[^rnnfeol]

You are given the root of a binary search tree (BST) and an integer val.

Find the node in the BST that the node’s value equals val and return the subtree rooted with that node. If such a node does not exist, return null.

Example 1

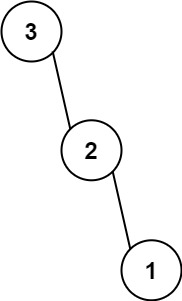
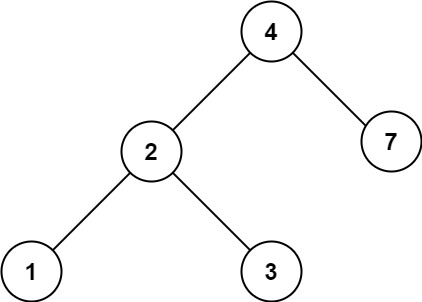
Input: root = [4,2,7,1,3], val = 2
Output: [2,1,3]

Example 2

Input: root = [4,2,7,1,3], val = 5
Output: []

Solution

A detailed explaination of solution can be found here⁶.

Python

class Solution(object):
    def searchBST(self, root, val):
        
        if root is None:
            return None
        
        if val == root.val:
            return root
        
        return self.searchBST(root.right,val) if val > root.val else self.searchBST(root.left,val)

Similar Questions

Diff	Similar Questions	Python	Java
	701 Insert into a Binary Search Tree7
	2476 Closest Nodes Queries in a Binary Search Tree8

Validate Binary Search Tree

Link to Leetcode question⁹

Given the root of a binary tree, determine if it is a valid binary search tree (BST).

A valid BST is defined as follows:

• The left subtree of a node contains only nodes with keys less than the node’s key.
• The right subtree of a node contains only nodes with keys greater than the node’s key.
• Both the left and right subtrees must also be binary search trees.

Example 1

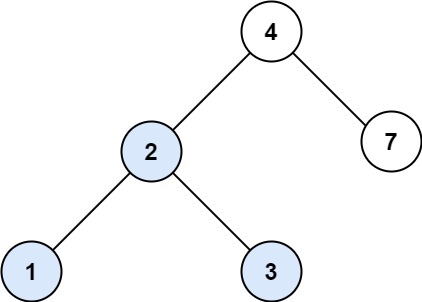
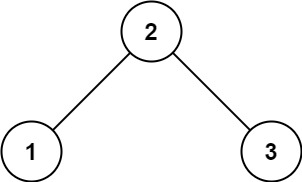
Input: root = [2,1,3]
Output: true

Example 2

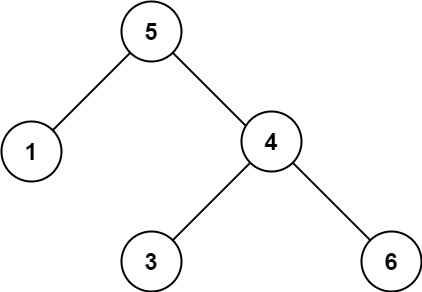
Input: root = [5,1,4,null,null,3,6]
Output: false
Explanation: The root node's value is 5 but its right child's value is 4.

Solution

A detailed explaination of solution can be found here¹⁰.

Python

class Solution(object):
    def isValidBST(self, root):
        que = []

        def inorder(node):
            if node is None:
                if len(que) > 0 and node.val <= que[-1]:
                    return False
                que.append(node.val)
                return True
            
            if node.left is not None:
                if not inorder(node.left):
                    return False
            
            if len(que) > 0 and node.val <= que[-1]:
                return False
            que.append(node.val)
            
            if node.right is not None:
                return inorder(node.right)
            
            return True

        return inorder(root)

Reference

1. Leetcode-654 Maximum Binary Tree: https://leetcode.com/problems/maximum-binary-tree/description/. ↩︎

2. 代码随想录-最大二叉树: https://programmercarl.com/0654.最大二叉树.html. ↩︎

3. Leetcode-998 Maximum Binary Tree II: https://leetcode.com/problems/maximum-binary-tree-ii/description/. ↩︎

4. Leetcode-617 Merge Two Binary Trees: https://leetcode.com/problems/merge-two-binary-trees/description/. ↩︎

5. 代码随想录-合并二叉树: https://programmercarl.com/0617.合并二叉树.html. ↩︎

6. 代码随想录-二叉搜索树中的搜索: https://programmercarl.com/0700.二叉搜索树中的搜索.html. ↩︎

7. Leetcode-701 Insert into a Binary Search Tree: https://leetcode.com/problems/insert-into-a-binary-search-tree/description/. ↩︎

8. Leetcode-2476 Closest Nodes Queries in a Binary Search Tree: https://leetcode.com/problems/closest-nodes-queries-in-a-binary-search-tree/description/. ↩︎

9. Leetcode-98 Validate Binary Search Tree: https://leetcode.com/problems/validate-binary-search-tree/description/. ↩︎

10. 代码随想录-验证二叉搜索树: https://programmercarl.com/0098.验证二叉搜索树.html. ↩︎