Leetcode Day 14 - Binary Tree: Path and Construction Problems

Binary Tree

Link to note about binary tree

Diff	Problem	Python	Java
	513 Find Bottom Left Tree Value	✅
	112 Path Sum	✅
	106 Construct Binary Tree from Inorder and Postorder Traversal	✅

Find Bottom Left Tree Value

Link to Leetcode question¹

Given the root of a binary tree, return the leftmost value in the last row of the tree.

Example 1

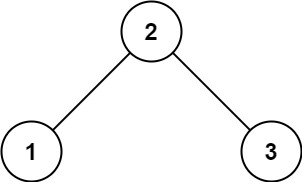
Input: root = [2,1,3]
Output: 1

Example 2

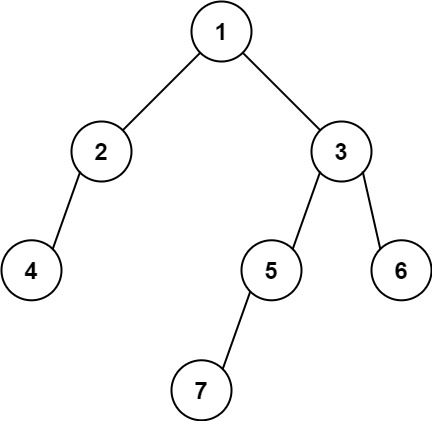
Input: root = [1,2,3,4,null,5,6,null,null,7]
Output: 7

Solution

A detailed explaination of solution can be found here².

Python

class Solution(object):
    def findBottomLeftValue(self, root):
                
        def find(node):
            if node is None:
                return None, 0
            
            if node.left is None and node.right is None:
                return node.val, 1
            
            if node.left is not None:
                left, left_depth = find(node.left)
                left_depth += 1
            
                if node.right is None:
                    return left, left_depth
                else:
                    right, right_depth = find(node.right)
                    right_depth += 1
                    if right_depth > left_depth:
                        return right, right_depth
                    else:
                        return left, left_depth
            right, right_depth = find(node.right)
            return right, right_depth + 1
        
        re, temp = find(root)
        return re

Path Sum

Link to Leetcode question³

Given the root of a binary tree and an integer targetSum, return true if the tree has a root-to-leaf path such that adding up all the values along the path equals targetSum.

A leaf is a node with no children.

Example 1

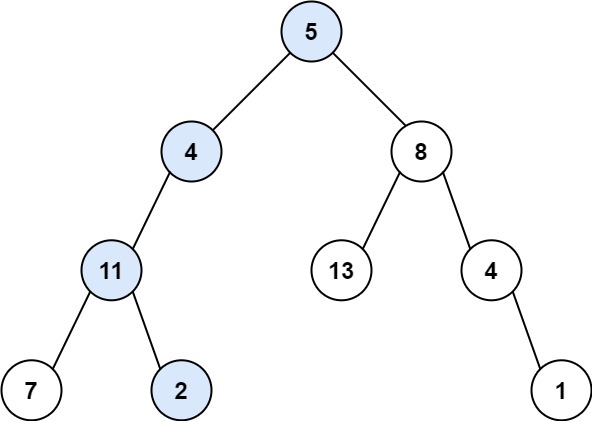
Input: root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
Output: true
Explanation: The root-to-leaf path with the target sum is shown.

Example 2

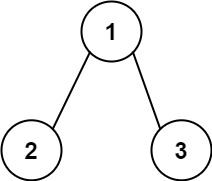
Input: root = [1,2,3], targetSum = 5
Output: false
Explanation: There two root-to-leaf paths in the tree:
(1 --> 2): The sum is 3.
(1 --> 3): The sum is 4.
There is no root-to-leaf path with sum = 5.

Example 3

Input: root = [], targetSum = 0
Output: false
Explanation: Since the tree is empty, there are no root-to-leaf paths.

Solution

A detailed explaination of solution can be found here⁴.

Python

class Solution(object):
    def hasPathSum(self, root, targetSum):

        def find(node,s):
            if node is None:
                return False
            
            if node.left is None and node.right is None and node.val == targetSum - s:
                return True
            
            s += node.val

            if node.left is not None:
                if find(node.left, s):
                    return True
            
            if node.right is not None:
                if find(node.right,s):
                    return True
            
            return False
    
        return find(root,0)

Similar Questions

Diff	Similar Questions	Python	Java
	113 Path Sum II5
	437 Path Sum III6
	124 Binary Tree Maximum Path Sum7

Construct Binary Tree from Inorder and Postorder Traversal

Link to Leetcode question⁸

Given two integer arrays inorder and postorder where inorder is the inorder traversal of a binary tree and postorder is the postorder traversal of the same tree, construct and return the binary tree.

Example 1

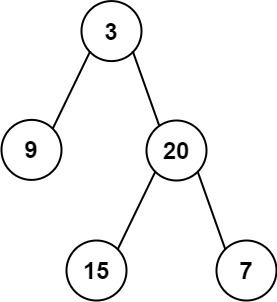
Input: inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
Output: [3,9,20,null,null,15,7]

Example 2

Input: inorder = [-1], postorder = [-1]
Output: [-1]

Solution

A detailed explaination of solution can be found here⁹.

Python

class Solution(object):
    def buildTree(self, inorder, postorder):

        def construct(inorder, postorder):
            if not inorder:
                return None

            mid = postorder.pop()
            i = inorder.index(mid)
            
            right_node = construct(inorder[i + 1:], postorder)
            left_node = construct(inorder[:i], postorder)

            return TreeNode(mid, left_node, right_node)
        
        return construct(inorder, postorder)

Similar Questions

Diff	Similar Questions	Python	Java
	105 Construct Binary Tree from Preorder and Inorder Traversal10

Reference

1. Leetcode-513 Find Bottom Left Tree Value: https://leetcode.com/problems/find-bottom-left-tree-value/description/. ↩︎

2. 代码随想录-找树左下角的值: https://programmercarl.com/0513.找树左下角的值.html. ↩︎

3. Leetcode-112 Path Sum: https://leetcode.com/problems/path-sum/description/. ↩︎

4. 代码随想录-路径总和: https://programmercarl.com/0112.路径总和.html. ↩︎

5. Leetcode-113 Path Sum II: https://leetcode.com/problems/path-sum-ii/description/. ↩︎

6. Leetcode-437 Path Sum III: https://leetcode.com/problems/path-sum-iii/description/. ↩︎

7. Leetcode-124 Binary Tree Maximum Path Sum: https://leetcode.com/problems/binary-tree-maximum-path-sum/description/. ↩︎

8. Leetcode-106 Construct Binary Tree from Inorder and Postorder Traversal: https://leetcode.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/description/. ↩︎

9. 代码随想录-从中序与后序遍历序列构造二叉树: https://programmercarl.com/0106.从中序与后序遍历序列构造二叉树.html. ↩︎

10. Leetcode-105 Construct Binary Tree from Preorder and Inorder Traversal: https://leetcode.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/. ↩︎