Leetcode Day 13 - Binary Tree: Tree Balance and Paths
Examines binary tree balance (height-balanced trees), finding all root-to-leaf paths, summing left leaves, and counting nodes in complete trees.
Binary Tree
| Diff | Problem | Python | Java |
|---|---|---|---|
 | 110 Balanced Binary Tree | ✅ | |
 | 257 Binary Tree Paths | ✅ | |
 | 404 Sum of Left Leaves | ✅ | |
 | 222 Count Complete Tree Nodes | ✅ |
Balanced Binary Tree
Given a binary tree, determine if it is height-balanced.
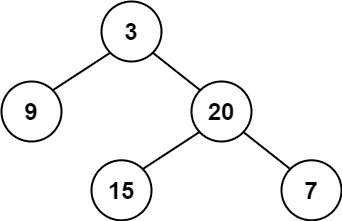
Example 1
1
2
Input: root = [3,9,20,null,null,15,7]
Output: true
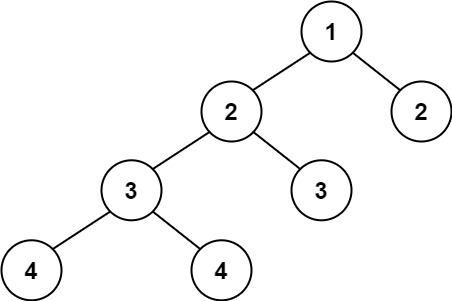
Example 2
1
2
Input: root = [1,2,2,3,3,null,null,4,4]
Output: false
Example 3
1
2
Input: root = []
Output: true
Solution
Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution(object):
def isBalanced(self, root):
def subtree(node):
if node is None:
return 0
if node.left is None and node.right is None:
return 1
if node.right is not None:
right_depth = subtree(node.right)
if right_depth == -2:
return -2
else:
right_depth = 0
if node.left is not None:
left_depth = subtree(node.left)
if left_depth == -2:
return -2
else:
left_depth = 0
if abs(left_depth - right_depth) > 1:
return -2
else:
return max(left_depth, right_depth) + 1
return False if subtree(root) == -2 else True
Binary Tree Paths
Given the root of a binary tree, return all root-to-leaf paths in any order.
A leaf is a node with no children.
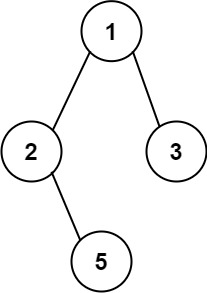
Example 1
1
2
Input: root = [1,2,3,null,5]
Output: ["1->2->5","1->3"]
Example 2
1
2
Input: root = [1]
Output: ["1"]
Solution
Similar Questions
Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution(object):
def binaryTreePaths(self, root):
if root is None:
return []
if root.left is None and root.right is None:
return [str(root.val)]
paths = []
def findPath(node, path):
if node is None:
return
path += "->" + str(node.val)
if node.left is None and node.right is None:
print(node.val, path)
paths.append(path)
return
findPath(node.left, path)
findPath(node.right, path)
findPath(root.left,str(root.val))
findPath(root.right,str(root.val))
return paths
| Diff | Similar Questions | Python | Java |
|---|---|---|---|
 | 113 Path Sum II5 | ||
 | 988 Smallest String Starting From Leaf[^psiisssfl |
Sum of Left Leaves
Given the root of a binary tree, return the sum of all left leaves.
A leaf is a node with no children. A left leaf is a leaf that is the left child of another node.
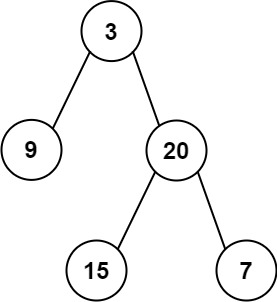
Example 1
1
2
3
Input: root = [3,9,20,null,null,15,7]
Output: 24
Explanation: There are two left leaves in the binary tree, with values 9 and 15 respectively.
Example 2
1
2
Input: root = [1]
Output: 0
Solution
Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution(object):
def sumOfLeftLeaves(self, root):
leaves = []
def traverse(node,isLeft):
if node is None:
return
if node.left is None and node.right is None:
if isLeft:
leaves.append(node.val)
return
traverse(node.left,True)
traverse(node.right, False)
traverse(root,False)
return sum(leaves)
Count Complete Tree Nodes
Given the root of a complete binary tree, return the number of the nodes in the tree.
According to Wikipedia, every level, except possibly the last, is completely filled in a complete binary tree, and all nodes in the last level are as far left as possible. It can have between 1 and 2h nodes inclusive at the last level h.
Design an algorithm that runs in less than O(n) time complexity.
Example 1
1
2
Input: root = [1,2,3,4,5,6]
Output: 6
Example 2
1
2
Input: root = []
Output: 0
Example 3
1
2
Input: root = [1]
Output: 1
Solution
Python
笔记后补
Solution 1
1
2
3
4
5
6
7
8
9
10
11
class Solution(object):
def countNodes(self, root):
if not root: return 0
count = 1
left = root.left; right = root.right
while left and right:
count+=1
left = left.left; right = right.right
if not left and not right:
return 2**count-1
return 1+self.countNodes(root.left)+self.countNodes(root.right)
Solution 2
1
2
3
4
5
class Solution(object):
def countNodes(self, root):
if not root:
return 0
return 1 + self.countNodes(root.left) + self.countNodes(root.right)
Reference
Leetcode-110 Balanced Binary Tree: https://leetcode.com/problems/balanced-binary-tree/description/. ↩︎
代码随想录-平衡二叉树: https://programmercarl.com/0110.平衡二叉树.html. ↩︎
Leetcode-257 Binary Tree Paths: https://leetcode.com/problems/binary-tree-paths/description/. ↩︎
代码随想录-二叉树的所有路径: https://programmercarl.com/0257.二叉树的所有路径.html. ↩︎
Leetcode-113 Path Sum II: https://leetcode.com/problems/path-sum-ii/description/. ↩︎
Leetcode-404 Sum of Left Leaves: https://leetcode.com/problems/sum-of-left-leaves/description/. ↩︎
代码随想录-左叶子之和: https://programmercarl.com/0404.左叶子之和.html#算法公开课. ↩︎
Leetcode-222 Count Complete Tree Nodes: https://leetcode.com/problems/count-complete-tree-nodes/description/. ↩︎
代码随想录-完全二叉树的节点个数: https://programmercarl.com/0222.完全二叉树的节点个数.html. ↩︎