Knuth-Morris-Pratt (KMP) Algorithm

String-matching algorithm

A string-matching algorithm wants to find the starting index m in string s that matches the search word w.¹ This process is foundational in text processing and computer science applications such as text editing and data retrieval.

Example

• s = "ABCABABCABDA"
• w "ABCABD"

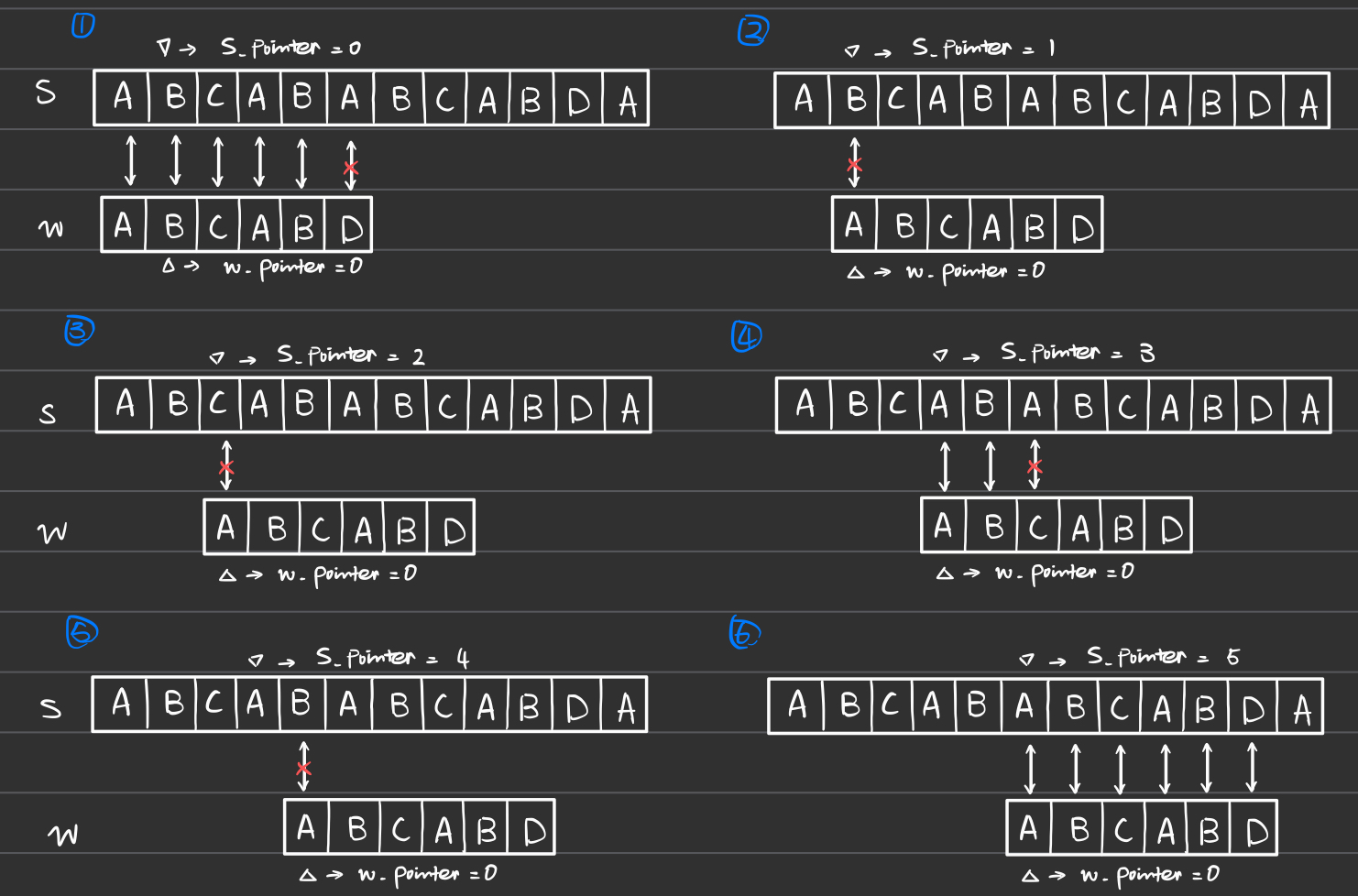
Brute force solution

The brute force approach employs a straightforward method using two pointers: one traverses the main string s and the other checks against the target word w. For each character in s, it compares the subsequent characters up to the length of w. If a mismatch occurs, the pointer in s moves to the next character, and the comparison begins anew.

However, this approach has a time complexity of O(mn), where m = len(s) and n = len(w). This method can become extremely inefficient, especially when mismatches consistently occur near the end of w and when w itself appears late in s. For example, consider s = "000000000000000000001" and w = "00000001". In this scenario, nearly every attempt will process almost the entire length of w before encountering a mismatch, leading to significant redundancy in the search process.

The advantage of KMP

The Knuth-Morris-Pratt (KMP) algorithm enhances efficiency through the use of a Prefix Table (aka. “Partial Match” Table¹) next. This table allows the algorithm to skip over sections of s that have previously been matched against parts of w, avoiding re-evaluation of characters that will anyway match according to the prefix table.

How KMP works

Prefixes and Suffixes

• Prefix Table:
  • This table is constructed from the search word w and records the length of the longest prefix which is also a suffix for the substring ending at each index i (inclusive).
  • Prefix:
    • A prefix of a string is any substring that starts at the beginning of the string and does not include the last character of the string. These are all possible leading segments of the string.
  • Suffix:
    • A suffix of a string is any substring that ends at the end of the string and does not include the first character of the string. These are all possible ending segments of the string².

 

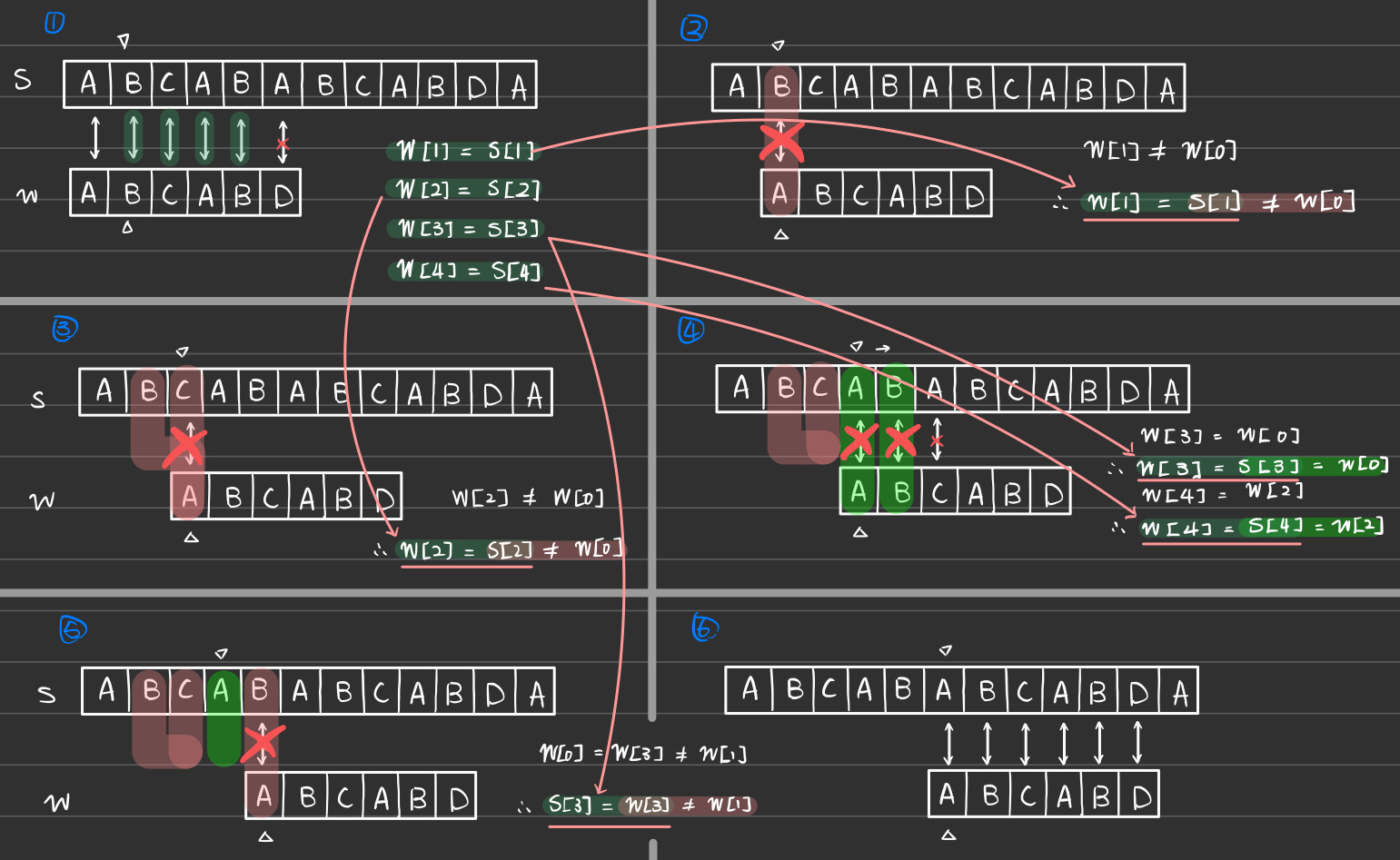
For each next[i] it record the longest prefix of w that matches a suffix ending just before w[i]. Instead of restarting the search from the next character in s, a prefix table next allows us to jump to w[next[i]], effectively bypassing the redundant re-checking of characters that are guaranteed to match based on previous comparisons.

Preprocessing: Create a prefix table

This preprocessing step involves the following three main stages:

1. Initialization
2. Handling Mismatches
3. Handling Matches

1. Initialization

First, create an array next of the same length as the pattern w and initialize all entries to 0.

get_next(w, next):
	next[0] = 0

After that, initialize pointers i = 1, j = 0 such that:

• i is the end of suffix and the next element in next to be updated .
• j is the end of prefix that is match with the suffix, and it also represent the length of the longest matched prefix and suffix.

2. Handling Mismatches

When the last element of the prefix s[j] mismatches with the end of the suffix w[i], we update the pointer j to find the next possible prefix length, and therefore move the j 1 step forward and look at the value of next in that position.

while j > 0 and w[i] != w[j]:
        j = next[j - 1]

There can be scenarios where even after falling back to a previous prefix length (j = next[j-1]), the new position of j still does not match the current character w[i]. Therefore, the while loop (while j > 0 and w[i] != w[j]) ensures that the algorithm continuously adjusts the length of the prefix being considered (j) until it either finds a matching prefix that can also match w[i] or exhausts all possible prefixes.

3. Handling Matches

When a match is found between w[i] and w[j] (w[i] == w[j]), it indicates that a prefix of length j ending at j-1 can be extended by one character (w[i]).

if w[i] == w[j]:
        j += 1

The complete code

get_next(w, next):
	next[0] = 0
  for i in range(1, len(w)):
      while j > 0 and w[i] != w[j]:
          j = next[j - 1]
      if w[i] == w[j]:
          j += 1
      next[i] = j

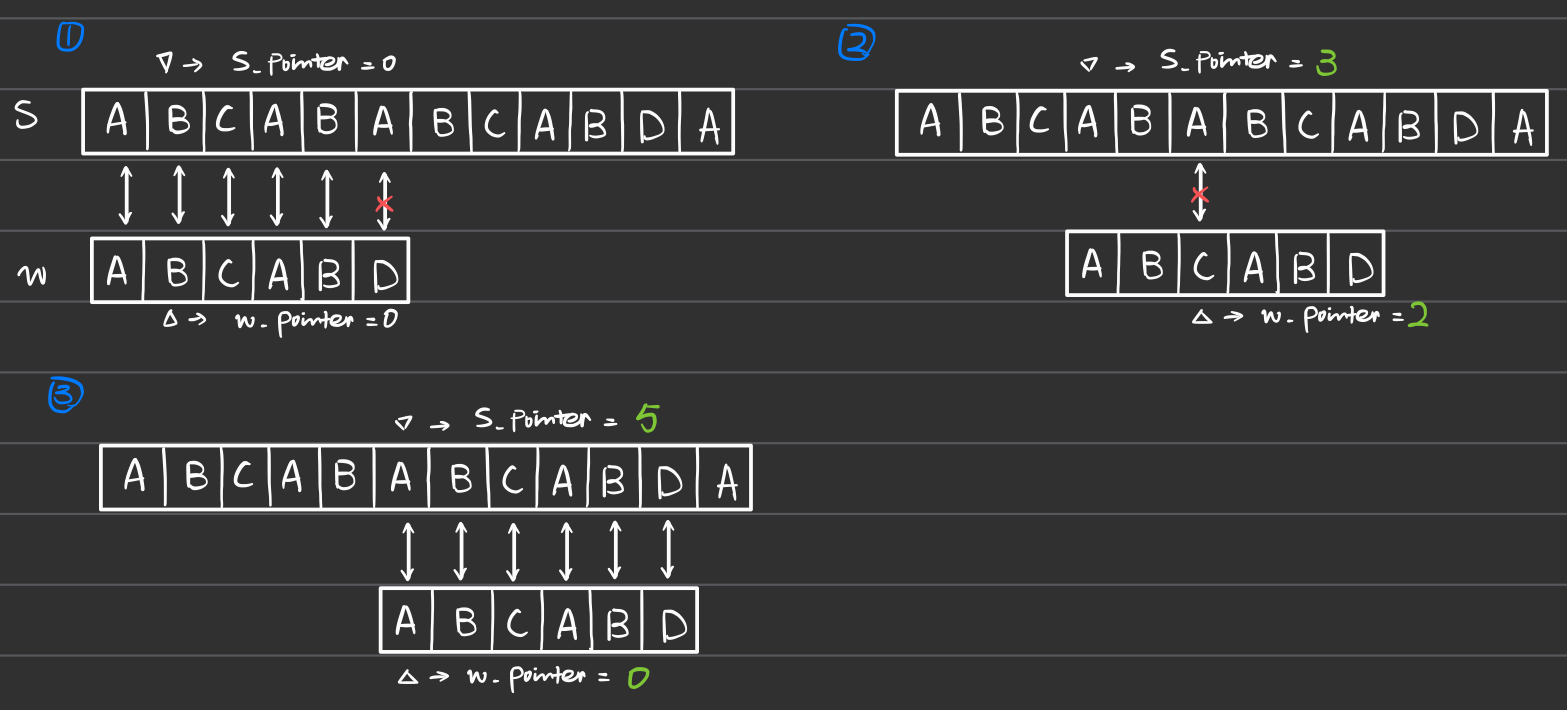
Searching: Align to the next potential match

How prefix table is used depends on the question itself. Some example questions that implement KMP are listed below:

Difficulty	Problem	Comment
	28 Find the Index of the First Occurrence in a String	Focuses on finding the first occurrence of a pattern within a longer text, a direct application of KMP’s quick search capabilities.
	459 Repeated Substring Pattern	Utilizes the prefix table to determine if the string can be constructed by repeating a substring, showcasing how KMP’s preprocessing can be adapted to solve complex pattern recognition problems.

Complexity of preprocessing

Since the preprocessing phase to build the prefix table and the subsequent search phase operate in O(n) and O(m) time respectively, where n is the length of the pattern w, and m is the length of the text s, the overall complexity of the KMP algorithm is O(n+m).

Reference

1. Wikipedia - Knuth–Morris–Pratt algorithm:https://en.wikipedia.org/wiki/Knuth–Morris–Pratt_algorithm. ↩︎ ↩︎²

2. 代码随想录: https://programmercarl.com/0028.实现strStr.html#思路 ↩︎