🍉🎃 第 3 章: 线性模型

思维导图

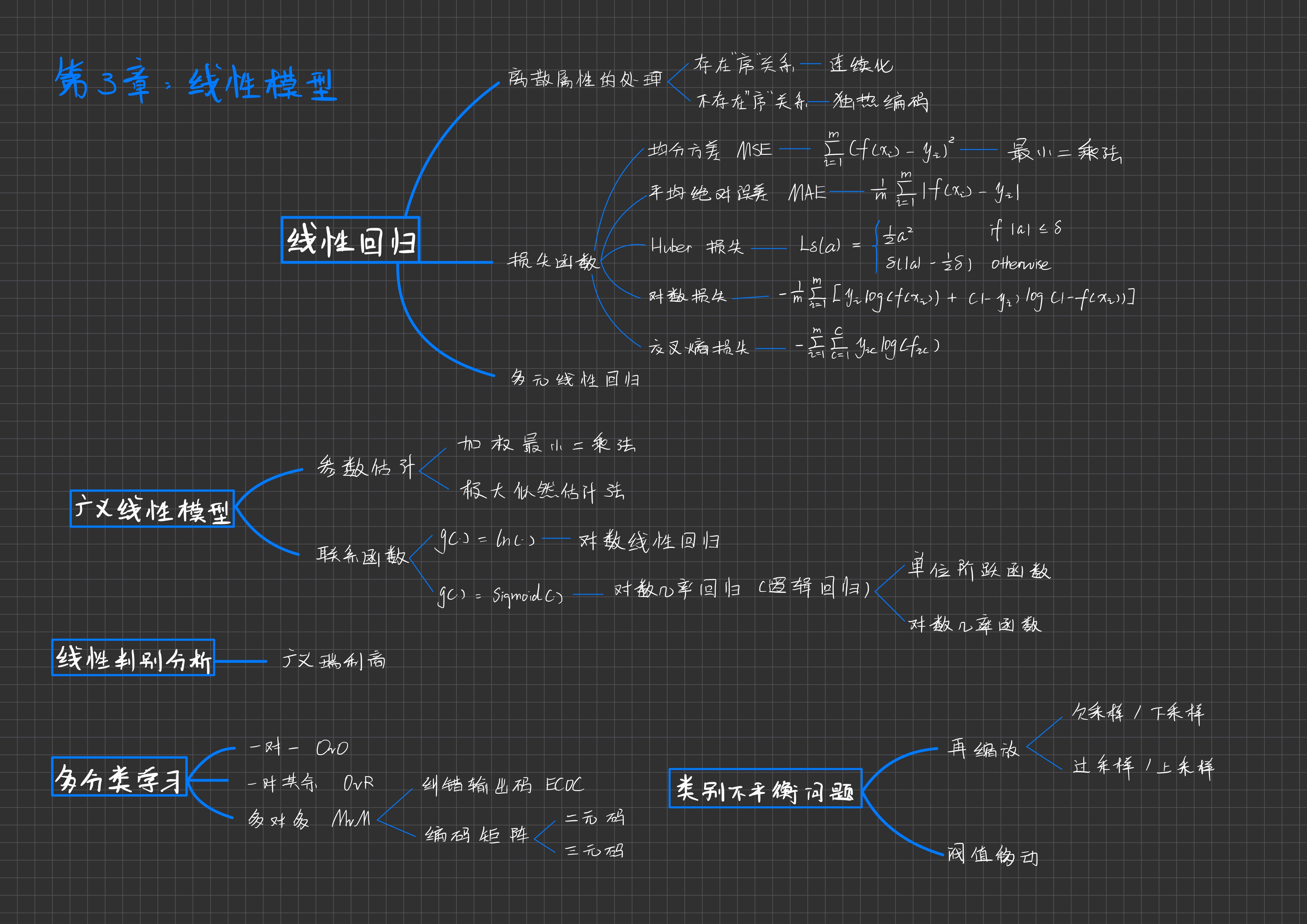
第3章思维导图

线性模型

给定一个包含 \(d\) 个属性的示例 \(x = (x_1, x_2, ..., x_d)\)，我们试图学习一个权重向量 \(\omega = (\omega_1, \omega_2, ..., \omega_d)\) 和偏置项 \(b\)，从而确定用于预测的线性函数。

线性模型的预测函数可以表示为：

\[f(x) = \omega_1 x_1 + \omega_2 x_2 + \dots + \omega_d x_d + b\]

一般情况下，可以用向量的形式简洁地表示为：

\[f(x) = \omega^T x + b\]

其中，\(\omega^T x\) 表示权重向量 \(\omega\) 和属性向量 \(x\) 的内积，\(b\) 为偏置项。

线性模型形式简单，易于建模，具有较强的可解释性（comprehensibility and understandability）。权重 \(\omega\) 直观地表示了各属性在预测中的重要性，因此也被称为权重（weight）。模型的每个权重可以解释该属性对预测结果的贡献。

---

线性回归 Linear regression

给定数据集 \(D = \{(x_1, y_1), (x_2, y_2), \dots, (x_m, y_m)\}\)，即 \(D = \{(x_i, y_i)\}_{i=1}^m\)，其中 \(x_i\) 为输入，\(y_i\) 为对应的输出值。线性回归的目标是通过数据集学习一个线性模型，用来预测新的数据点。

• 对存在“序”(order)关系的离散属性：
  • 通过连续化江其转化为连续值
  • 例如，属性“高度”具有“高”、“中”、“低”三个离散取值，但它们之间存在序关系，可以将其转化为连续值，如 {1.0, 0.5, 0.0}。
• 对不存在“序”关系的离散属性：
  • 若对无序属性进行连续化，会不恰当地引入序关系，可能导致误导性的处理（如在距离计算中）。通常，将 \(k\) 个无序属性值转化为 \(k\) 维向量（也称为“独热编码”或“one-hot encoding”）。
  • 例如，属性“类别”取值为“A”、“B”、“C”，可以将其编码为 (0, 0, 1)、(0, 1, 0)、(1, 0, 0)，而不会引入错误的顺序关系。

序 Order：序关系指属性值之间存在先后或大小关系。例如，“高”、“中”、“低”有明显的序关系，而“红”、“绿”、“蓝”则没有序关系。

线性回归试图学习如下形式的线性模型：

\[f(x_i) = \omega^T x_i + b\]

线性回归的目标是使模型 \(f(x_i)\) 对应的预测值尽可能接近真实值 \(y_i\)，即：

\[f(x_i) \approx y_i\]

损失函数 cost function

均分方差 Mean Square Error (MSE)

均分方差也称为平方损失函数 (Square Loss)。这一损失函数对应了常用的欧几里得距离（简称“欧氏距离” Euclidean distance）。损失函数定义为：

\[(\omega^*, b^*) = \underset{\omega, b}{\arg\min} \sum_{i=1}^{m} (f(x_i) - y_i)^2\]

MSE 对大误差惩罚较大，适用于误差服从正态分布的场景。

平均绝对误差 Mean Absolute Error (MAE)

计算预测值与真实值的绝对差值，公式如下：

\[\text{MAE} = \frac{1}{m} \sum_{i=1}^{m} |f(x_i) - y_i|\]

MAE 对离群点敏感度较低，适用于含有噪声或离群点的数据集。

Huber 损失 Huber Loss

结合了 MSE 和 MAE 的优点，适用于既包含小误差又包含离群点的场景：

\[L_{\delta}(a) = \begin{cases} \frac{1}{2}a^2 & \text{if } |a| \leq \delta \\ \delta(|a| - \frac{1}{2}\delta) & \text{otherwise} \end{cases}\]

其中 \(a = f(x_i) - y_i\)， \(\delta\) 是调节参数。

对数损失 Logarithmic Loss (Log Loss)

用于分类任务，尤其是二分类问题。计算模型预测的概率与真实标签之间的差异：

\[\text{Log Loss} = -\frac{1}{m} \sum_{i=1}^{m} \left[ y_i \log(f(x_i)) + (1 - y_i) \log(1 - f(x_i)) \right]\]

交叉熵损失 Cross Entropy Loss

用于多分类问题，衡量模型预测的类别分布与真实分布之间的差异：

\[\text{Cross Entropy} = -\sum_{i=1}^{m} \sum_{c=1}^{C} y_{ic} \log(f_{ic})\]

其中 \(C\) 是类别数，\(y_{ic}\) 是样本 \(i\) 的真实类别，\(f_{ic}\) 是预测概率。

最小二乘法 least square method

最小二乘法是一种优化策略，目的是最小化均方误差。通过最小化损失函数，最小二乘法能够找到最优的参数 \(\omega\) 和 \(b\)，从而使得模型的预测值与真实值之间的差异最小。这一优化过程通常被称为线性回归模型的最小二乘参数估计 (parameter estimation)。

多元线性回归 Multiple linear regression

当样本由 \(d > 1\) 个属性描述时，多元线性回归模型可以表示为：

\[f(x_i) = \omega^T x_i + b\]

通过最小化损失函数找到最优的 \(\omega\)，多元线性回归的参数估计公式为：

\[\hat{\omega} = \underset{\omega}{\arg\min} \ (y - X\hat{\omega})^T (y - X\hat{\omega})\]

---

广义线性模型 Generalized Linear Model (GLM)

广义线性模型扩展了线性回归的框架，允许通过联系函数 (Link Function) 来处理不同类型的输出变量。GLM 的模型形式为：

\[y = g^{-1}(\omega^T x + b)\]

其中，\(g(·)\) 是联系函数，通常是一个单调可微的函数，用来连接输入变量的线性组合与输出变量的期望值。联系函数是连续且充分光滑的，能够将线性模型应用于更广泛的问题，如分类、计数数据和比例数据。

参数估计

在广义线性模型中，参数 \(\omega\) 和 \(b\) 通常通过以下两种方法进行估计：

加权最小二乘法 Weighted Least Squares (WLS)

加权最小二乘法是广义线性模型中常用的一种参数估计方法，特别适用于数据中方差不恒定的情况。与普通最小二乘法不同，加权最小二乘法通过为每个数据点赋予一个权重，以反映其重要性或不确定性。其目标是最小化加权平方误差，即：

\[(\omega^*, b^*) = \underset{\omega, b}{\arg\min} \sum_{i=1}^{m} w_i (y_i - f(x_i))^2\]

其中，\(w_i\) 是每个数据点的权重，反映了该点的方差。加权最小二乘法在处理异方差（方差随输入值变化）时非常有效。

极大似然估计法 Maximum Likelihood Estimation (MLE)

极大似然估计法是一种广泛应用于统计模型中的参数估计方法，用于在给定观测数据的情况下，找到最有可能产生这些数据的模型参数。对于广义线性模型，极大似然估计通过最大化似然函数 \(L(\omega, b)\) 来估计模型参数：

\[(\omega^*, b^*) = \underset{\omega, b}{\arg\max} \ L(\omega, b)\]

似然函数 \(L\) 是基于数据点的联合概率分布构建的。通过最大化似然函数，可以找到最能解释观测数据的参数组合。极大似然法是许多统计模型中的标准方法，尤其在处理带有随机误差的数据时表现优越。

• 应用场景：在广义线性模型中，MLE 特别适用于当输出变量来自于某种概率分布（如二项分布或泊松分布）时。它能够为分类问题（如逻辑回归）或计数数据建模提供有效的参数估计。

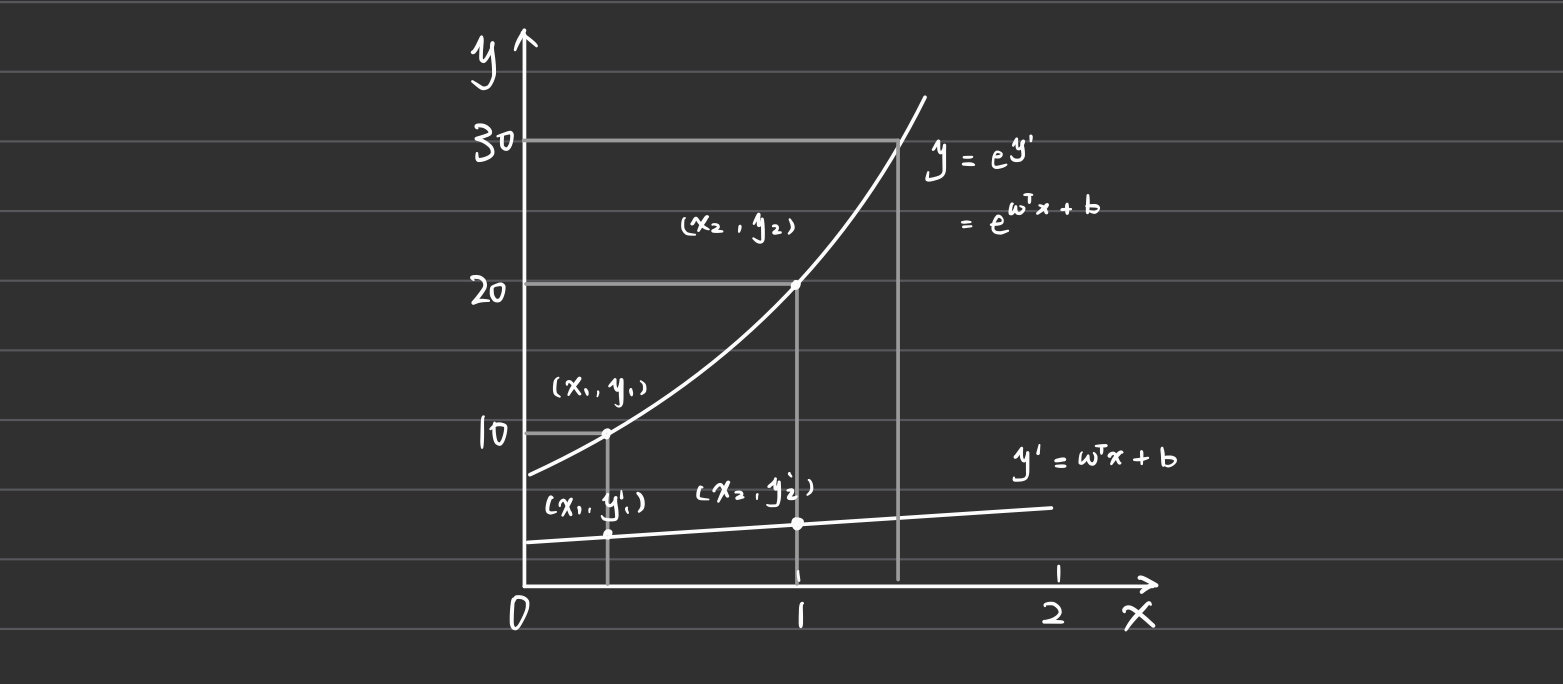
对数线性回归 Log-Linear Regression

对数线性回归时光一线性模型在 \(g(·) = ln(·）\) 时的特例。在对数线性回归中，模型的目标是让 \(e^{\omega^T x_i + b}\) 逼近 \(y\)。虽然形式上仍然是线性回归，但通过对预测值 \(y\) 进行指数运算，模型实际上是在求输入空间到输出空间的非线性函数映射：

\[f(x_i) = e^{\omega^T x_i + b}\]

对数线性回归

这种模型常用于处理对数分布的目标变量，尤其是在处理某些特定类型的计数数据或概率时非常有效。形式上属于广义线性模型的一部分，但由于输出值是非线性函数的结果，因此实质上是一种非线性回归。

对数几率回归 逻辑回归 Logistic Regression

逻辑回归是一种分类模型，它将实值 \(z = \omega^T x + b\) 转换为 0/1 的分类结果。

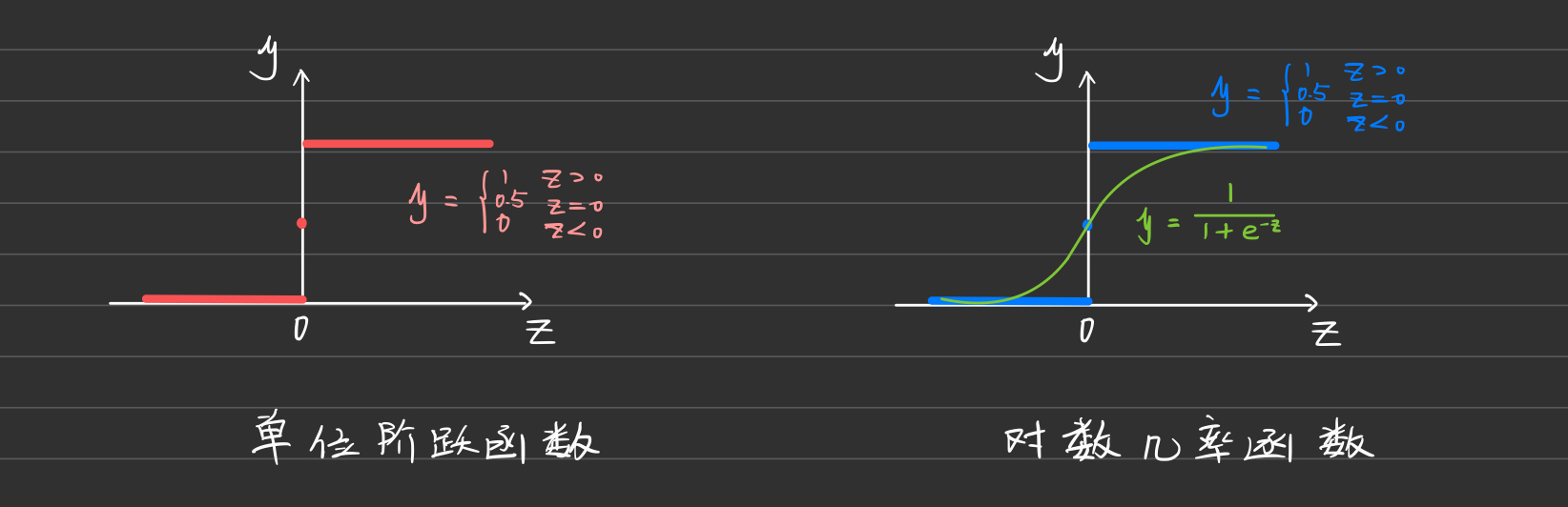
单位阶跃函数 Unit Step Function

单位阶跃函数将实值 \(z\) 转换为离散的 0 或 1 值：

\[y = \begin{cases} 0 & \text{if } z < 0 \\ 0.5 & \text{if } z = 0 \\ 1 & \text{if } z > 0 \end{cases}\]

缺点：单位阶跃函数不连续，无法用于模型的优化（如梯度下降），因为它不可导。

对数几率函数 Logistic function

对数几率函数是单调可微的，能够在一定程度上近似单位阶跃函数。它将实值 \(z\) 映射为 0 到 1 之间的概率值：

\[y = \frac{1}{1 + e^{-z}}\]

这是逻辑回归中常用的Sigmoid函数，其输出值可以解释为样本属于正类的概率。

单位阶跃函数与对数几率函数示意图

Sigmoid函数还可以表示为：

\[\ln \frac{y}{1 - y} = \omega^T x + b\]

其中，\(y\) 表示样本为正例的概率，\(1 - y\) 表示样本为反例的概率。两者的比值 \(\frac{y}{1 - y}\) 称为几率 (odds)，反映了样本作为正例的相对可能性。对几率取对数得到 对数几率 (log odds)：

\[\ln \frac{y}{1 - y}\]

当 \(y\) 被解释为样本作为正例的概率时，\(\frac{y}{1 - y}\) 就是正例和反例的概率比值。对几率取对数后，得到的结果与输入特征的线性组合 \(\omega^T x + b\) 线性相关。

逻辑回归的特点

• 概率建模：逻辑回归不仅仅给出分类结果，还能提供类别的概率估计。
• 可导性：对数几率函数是一个任意阶可导的凸函数，适合使用梯度下降等优化方法进行训练。
• 无需假设数据分布：逻辑回归无需像朴素贝叶斯那样对数据的分布作假设，因此更加灵活，适用于各种分类问题。

---

线性判别分析 Linear Discriminant Analysis (LDA)

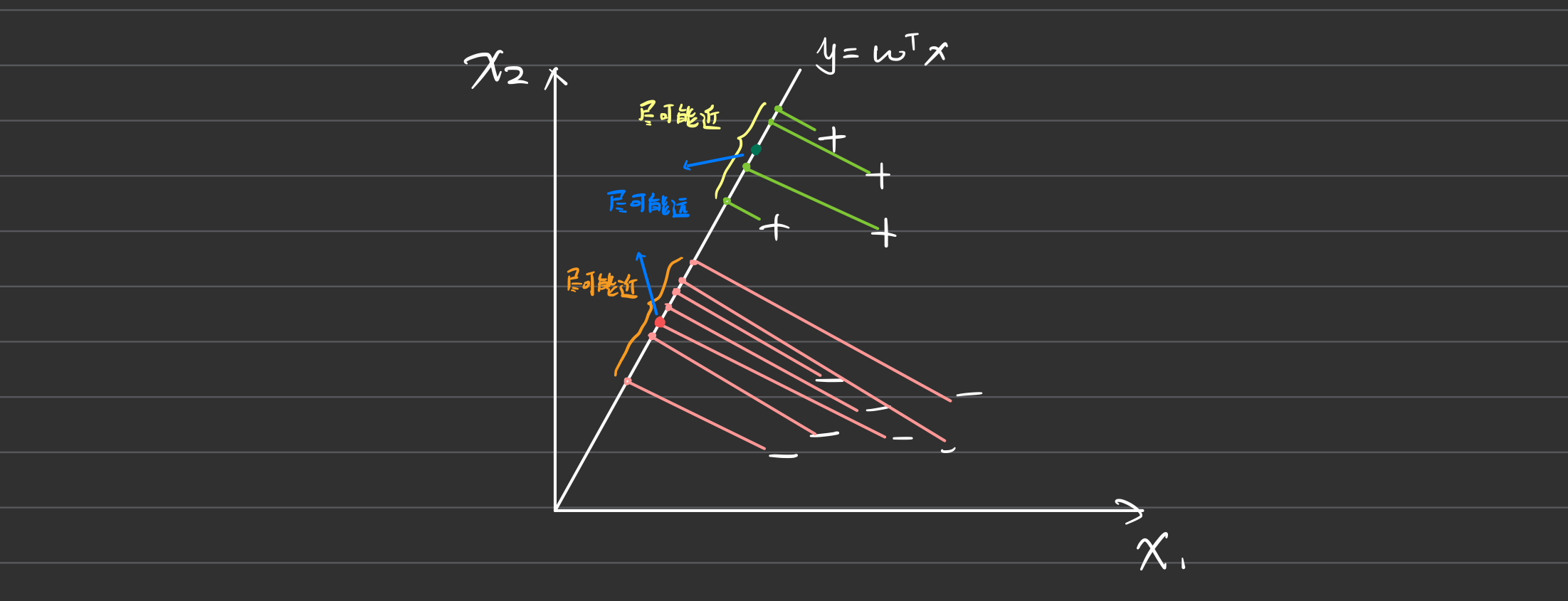
LDA 是由 Fisher 提出的判别分析方法，因此又称为 Fisher 判别分析。其目标是在给定训练样例集的情况下，找到一条直线，将样例投影到该直线上，使得同类样例的投影点尽可能接近，而不同类样例的投影点尽可能远离。

线性判别分析示意图

LDA 的基本原理

给定数据集 \(D = \{(x_i, y_i)\}_{i=1}^m\)，其中 \(y_i \in \{0, 1\}\)。

• \(x_i\)：第 \(i\) 类（\(0\) 或 \(1\)）的样本集合。
• \(\mu_i\)：类 \(i\) 样本的均值向量。
• \(\Sigma_i\)：类 \(i\) 样本的协方差矩阵。

在 LDA 中，我们希望通过线性投影 \(\omega\)，使两类样本的中心在直线上的投影为 \(\omega^T \mu_i\)，而所有样本点投影到直线上的协方差为 \(\omega^T \Sigma_i \omega\)。

根据线性判别分析的定义，得到以下优化目标：

1. 最小化同类样例的投影点差异
   • 最小化同类样例投影点的协方差： \(\arg\min_{\omega} \omega^T \Sigma_0 \omega + \omega^T \Sigma_1 \omega\)
2. 最大化异类样例投影点之间的距离
   • 最大化两类中心的投影距离： \(\arg\max_{\omega} || \omega^T \mu_0 - \omega^T \mu_1 ||^2_2\)

LDA 的优化目标函数可以表示为：

\[J(\omega) = \frac{|| \omega^T (\mu_0 - \mu_1) ||^2_2}{\omega^T (\Sigma_0 + \Sigma_1) \omega}\]

广义瑞利商 Generalized Rayleigh Quotient

在 LDA 中，广义瑞利商是用于衡量类间散度和类内散度的比值，其目标是最大化类间散度，同时最小化类内散度。

类内散度矩阵 Within-class Scatter Matrix

类内散度矩阵用于度量同一类样本在投影方向上的分散程度，定义为所有类的类内散度之和：

\[S_w = \Sigma_0 + \Sigma_1 = \sum_{x \in X_0} (x - \mu_0)(x - \mu_0)^T + \sum_{x \in X_1} (x - \mu_1)(x - \mu_1)^T\]

类间散度矩阵 Between-class Scatter Matrix

类间散度矩阵用于衡量两类样本的中心之间的距离，定义为两个类均值之间的距离：

\[S_b = (\mu_0 - \mu_1)(\mu_0 - \mu_1)^T\]

类间散度矩阵反映了两类样本的中心（均值向量）之间的差异。

更新线性判别的损失函数

根据类内散度矩阵和类间散度矩阵，LDA 的优化目标函数 \(J\) 可以重写为：

\[J(\omega) = \frac{\omega^T S_b \omega}{\omega^T S_w \omega}\]

---

多分类学习 Multiclass Learning

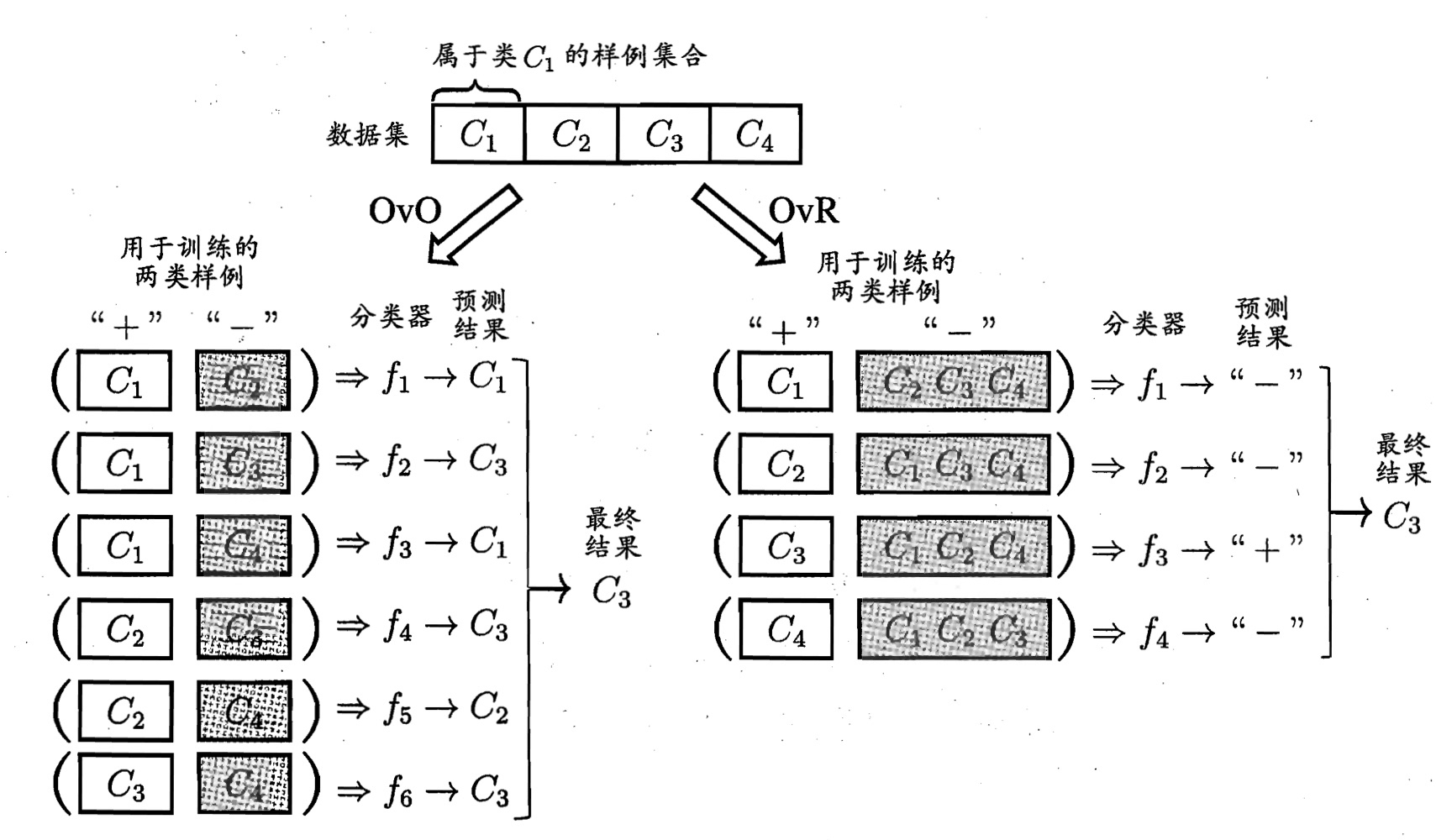
在多分类学习中，考虑有 \(N\) 个类别，记为 \(C_1, C_2, \dots, C_N\)。多分类学习的基本思路是“拆解法”，即将多分类问题分解为多个二分类问题来分别训练分类器，然后对这些分类器的预测结果进行集成，以获得最终的分类结果。

一对一 OvO 与一对其余 OvR

一对一 One vs One (OvO)

将 \(N\) 个类别两两配对，生成 \(\frac{N(N-1)}{2}\) 个二分类任务。对于每个二分类问题，训练一个分类器。最终的分类结果由投票机制决定：被预测最多的类别作为最终的分类结果。

一对其余 One vs Rest (OvR)

每次将一个类别的样本作为正例，其余类别的样本作为反例，生成 \(N\) 个二分类任务。对于每个二分类问题，训练一个分类器。如果有多个分类器预测样本为正类，则通常通过比较各分类器的预测置信度来决定最终的分类结果。

OvO 与 OvR 的比较

• 存储和测试开销：OvO 的存储和测试时间开销通常比 OvR 更大，因为 OvO 需要训练和存储更多的分类器。

• 训练开销：当类别很多时，OvO 的每个分类器仅使用两个类别的样本，因此训练开销比 OvR 小。

• 总结：OvO 适用于类别较多的情况，而 OvR 适用于类别较少或需要较少存储空间的情况。

OvO 与 OvR 示意图（原图来自西瓜书 图3.4）

多对多 Many vs Many (MoM)

在 多对多 方法中，每次将若干个类别作为正类，若干个类别作为反类，构建多个二分类问题，最终组合这些分类器的结果以进行多分类任务。

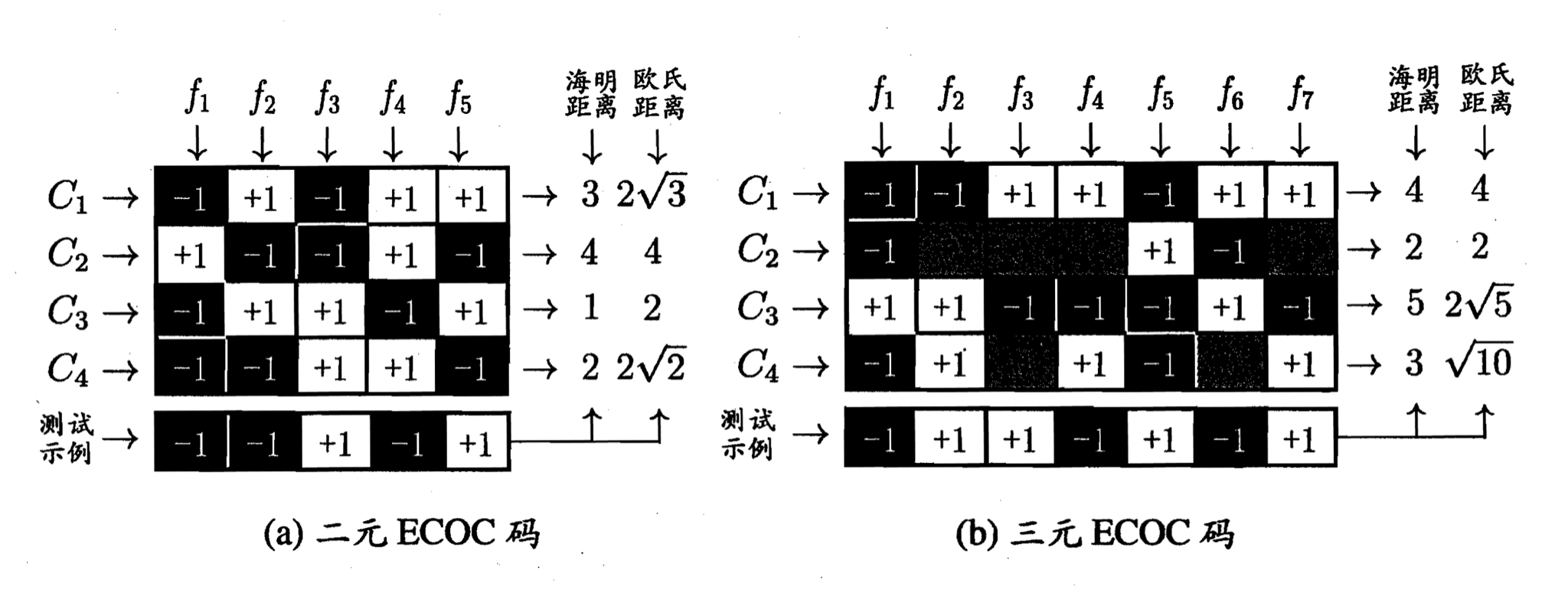
纠错输出码 Error conecting output codes (ECOC)

纠错输出码的工作过程主要分为以下两步：

1. 编码：对 \(N\) 个类别进行 \(M\) 次划分，从而产生 \(M\) 个训练集，用于训练 \(M\) 个分类器。
2. 解码：将 \(M\) 个分类器的预测结果组成一个编码，并与每个类别的预设编码进行比较。选择距离最小的编码所对应的类别作为最终预测结果。

编码矩阵 Coding Matrix

类别划分通过编码矩阵来制定，常见的划分形式有：

• 二元码 (Binary Code)：将每个类别分别指定为正类 (+1) 和反类 (-1)。
• 三元码 (Ternary Code)：将每个类别分别指定为正类 (+1)、反类 (-1) 和停用类 (0)。

ECOC编码示意图（原图来自西瓜书 图3.5）

ECOC 的特点

ECOC 对分类器的错误有一定的容错和修正能力。一般来说，ECOC 编码越长，纠错能力越强。然而，编码越长，计算和存储开销也越大。

理论上，同等长度的编码中，任意两个类别之间的编码距离越远，则纠错能力越强。因此，设计合理的编码矩阵对于提升分类器的准确率至关重要。

---

类别不平衡问题 Class Imbalance Problem

在分类任务中，不同类别的训练样例数量可能相差很大，这会导致分类器在预测时倾向于多数类，忽略少数类，影响少数类的识别效果。即使在原始问题中，不同类别的训练样例数量相近，在使用 OvR（One-vs-Rest）或 MvM（Many-vs-Many）方法后，产生的二分类任务中仍可能出现类别不平衡现象。

再缩放 Rescalling

再缩放方法（亦称再平衡，Rebalance）通过对训练数据的分布进行调整来应对类别不平衡问题。再缩放方法分为欠采样和过采样两种策略。

欠采样 Oversampling

欠采样（亦称下采样，Downsampling）是通过去除一些多数类样本，使得正反例数目相近。这种方法时间开销较小，但训练集规模会变小，如果随意丢弃样例，可能会丢失重要信息。

• 代表性算法：Easy Ensemble
  • 通过集成学习机制，将多数类样例划分为若干个子集，每个子集与少数类样例结合，训练不同的学习器，最后集成它们的结果。

过采样 Oversampling

过采样（亦称上采样，Upsampling）通过增加少数类样本使得正反例数目相近。但不能简单地通过重复采样来增加样例，否则会导致模型的过拟合。

• 代表性算法：SMOTE (Synthetic Minority Over-sampling Technique)
  • SMOTE 通过对少数类样例进行插值来生成新的样本。插值是指在少数类样本的特征空间中，选择两个或多个样本点之间的点生成新的样例，这样可以有效避免过拟合，并增强模型对少数类的识别能力。

阀值移动 Threshold-moving

阈值移动方法直接通过调整分类器的决策阈值来应对类别不平衡问题。通常分类器会使用 0.5 作为分类阈值，但在类别不平衡的情况下，这个默认的阈值可能不适合少数类。

• 提高正类阈值：使得模型更容易将样本判定为少数类，从而提升少数类的召回率。
• 降低负类阈值：使得模型更容易将样本判定为多数类，减少对少数类的误分类。

阈值移动方法不改变训练数据本身，而是调整分类器的输出决策。

对数几率回归中的阈值调整

回顾对数几率回归中，sigmoid 函数为：

\[\ln \frac{y}{1 - y} = \omega^T x + b\]

当 \(\ln \frac{y}{1 - y} > 0\)，即 \(\frac{y}{1 - y} > 1\) 时，预测为正类。这实际上默认了正、反类的数量相似，因此将分类阈值设置为 0.5。

当训练集中正反类样本数量分别为 \(m^+\) 和 \(m^-\) 时，阈值移动方法通过调整对数几率函数的决策边界，改变阈值以适应样本数量的不平衡。新的对数几率关系为：

\[\frac{y'}{1 - y'} = \frac{y}{1 - y} \times \frac{m^-}{m^+}\]