Binary Tree
Write down description here.
Table of Content
Related Leetcode Questions
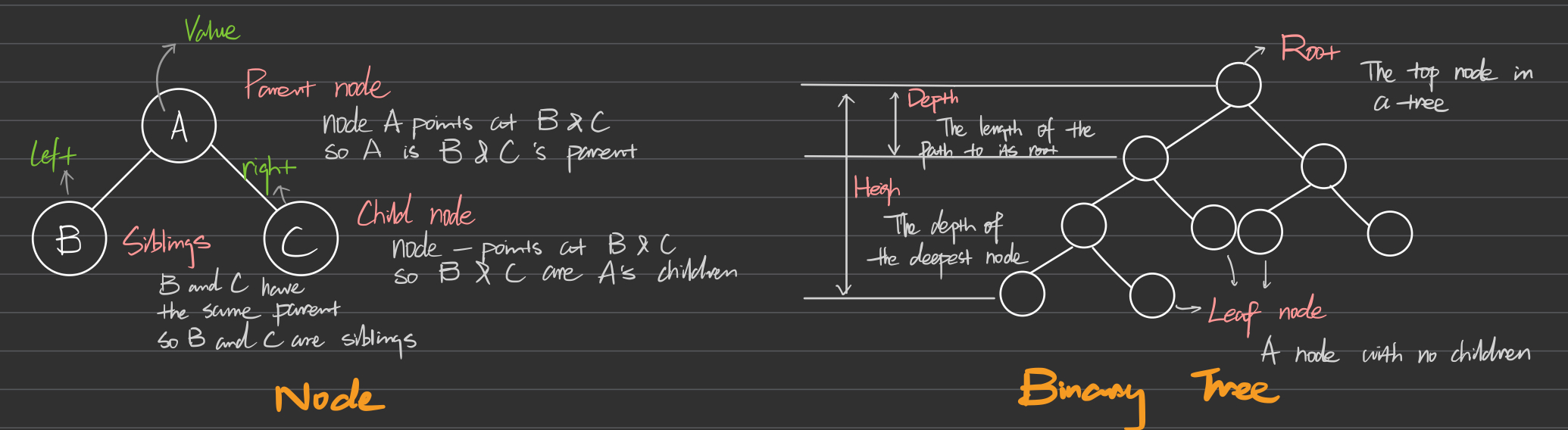
How binary trees are stored in memory
Binary trees can be stored in memory using two common representations: pointer-based (linked) structures and array-based structures.
Pointer-Based Storage (Linked Storage)
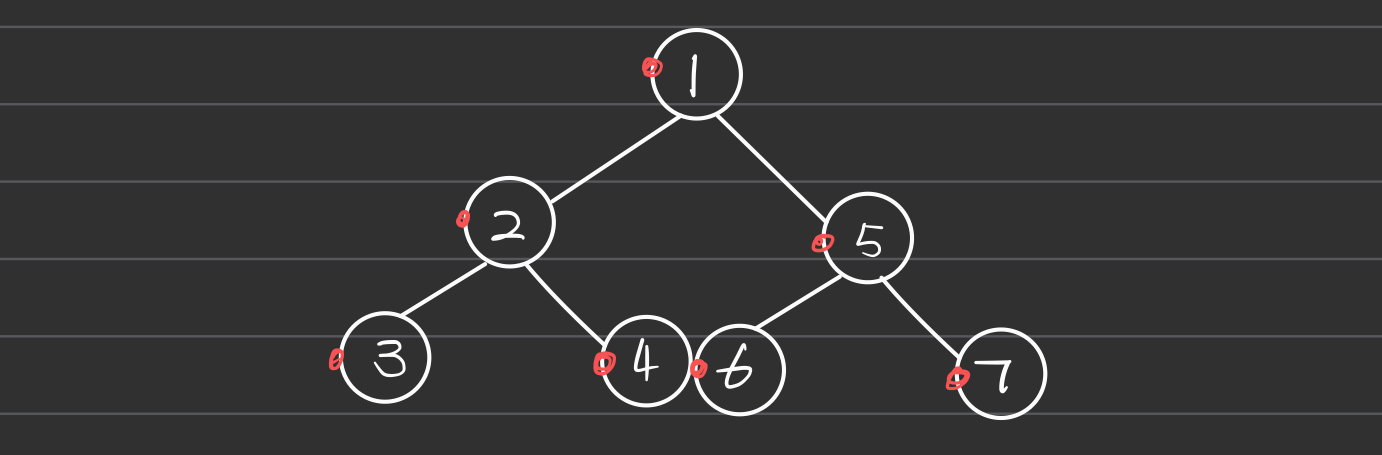
In pointer-based storage, each node is an object, and each node typically contains:
- Data: The value or information contained in the node.
- Left Child Pointer: A pointer to the left child node.
- Right Child Pointer: A pointer to the right child node.
1
2
3
4
5
class BinaryTree:
def __init__(self, value):
self.val = value # The value or information contained in the node.
self.left = None # A pointer to the left child node.
self.right = None # A pointer to the right child node.
This method is dynamic, allowing the tree to expand as needed. It is particularly useful for operations that involve frequent insertions and deletions, as nodes can be added or removed without reorganizing the entire structure.
Array-Based Storage
In array-based storage of binary trees:
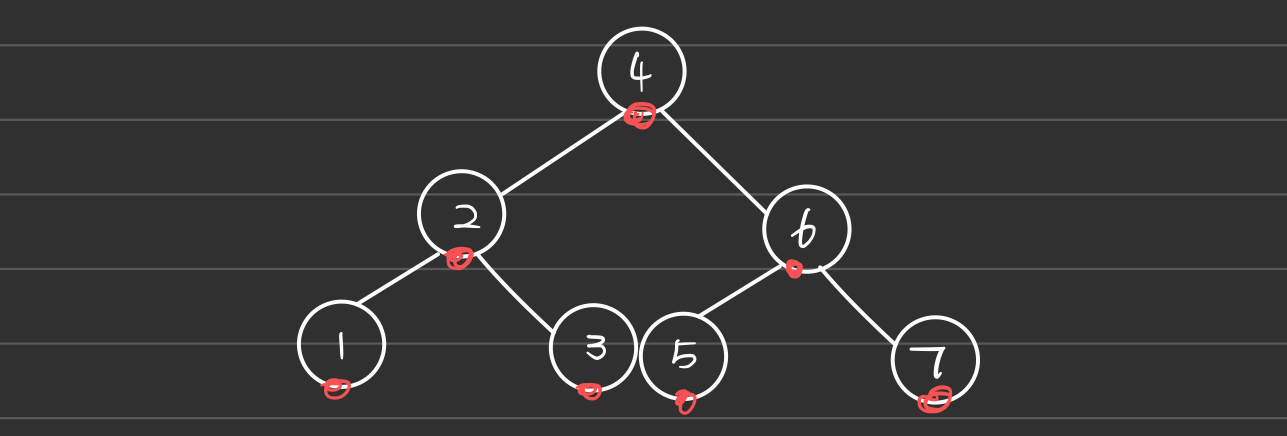
- Root: The root element is stored at the beginning of the array.
- Left Child: The left child of a node located at position n is found at position 2n + 1.
- Right Child: The right child of a node located at position n is found at position 2n + 2.
This method is space-efficient when the tree is complete and perfect, as it doesn’t require any pointers. However, for sparse trees, this method can waste memory space due to empty indices in the array representing absent nodes.
Array storage is particularly efficient for binary heaps and other binary trees that require accessing children and parents in constant time during insertions and deletions.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class ArrayBasedBinaryTree:
def __init__(self):
self.tree = [] # Initialize an empty list to store tree elements
def root(self, value):
"""Insert root node"""
if not self.tree:
self.tree.append(value) # Insert root if tree is empty
def insert_left(self, parent_index, value):
"""Insert left child"""
child_index = 2 * parent_index + 1
if child_index < len(self.tree):
self.tree[child_index] = value
else:
# Extend the list with None to maintain structure
while len(self.tree) <= child_index:
self.tree.append(None)
self.tree[child_index] = value
def insert_right(self, parent_index, value):
"""Insert right child"""
child_index = 2 * parent_index + 2
if child_index < len(self.tree):
self.tree[child_index] = value
else:
# Extend the list with None to maintain structure
while len(self.tree) <= child_index:
self.tree.append(None)
self.tree[child_index] = value
def display(self):
"""Display the tree"""
return self.tree
Different types of binary tree
Different types of binary trees are designed to meet specific needs, such as maintaining balance or optimizing search operations.
| Binary Tree | Applications |
|---|---|
| Full Binary Trees | Often used in applications that require a simple and efficient tree structure without complex operations. |
| Complete Binary Trees | Ideal for priority queues and heap-based algorithms, where quick access to elements is necessary. |
| Binary Search Trees (BST) | Serve well in database indexing systems where quick insertion, deletion, and retrieval of records are frequent. |
| AVL Trees | In applications where low latency data retrieval is critical, such as in network routers, where balancing ensures optimal search times. |
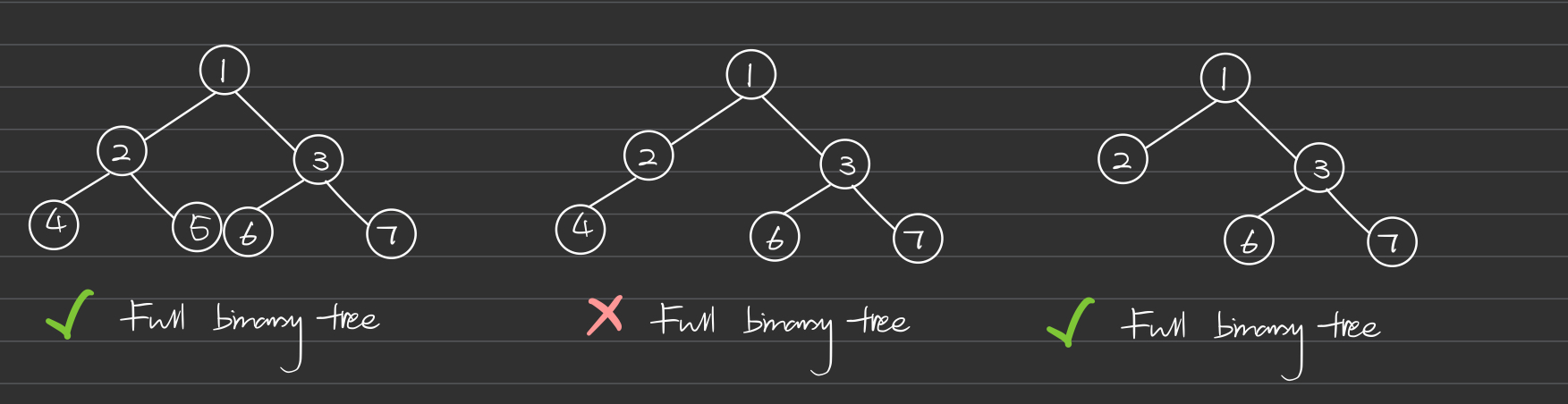
Full Binary Tree
A full binary tree is a type of binary tree in which every node other than the leaves has two children. In other words, each node has exactly zero or two children.
- Every node has 0 or 2 children.
- Leaves are at the same level or one level apart.
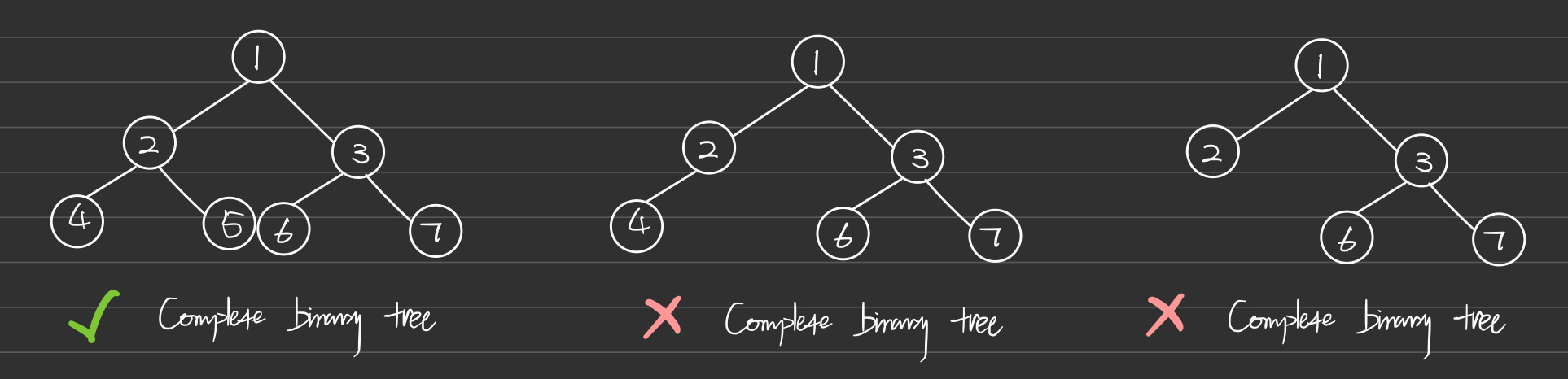
Complete Binary Tree
A complete binary tree is a type of binary tree in which all levels, except possibly the last, are completely filled, and all nodes are as left as possible. This arrangement makes complete binary trees ideal for being stored in an array, as their compact and left-filled structure reduces the space complexity.
- All levels are fully filled except possibly the last level.
- Nodes are positioned as far left as possible.
Binary Search Tree (BST)
A binary tree in which for each node, the left children are less than the node and the right children are greater. This property makes BSTs immensely useful for search and retrieval operations, as the decision tree of going left or right at each step significantly cuts down the search space.
- The left subtree of a node contains only nodes with keys lesser than the node’s key.
- The right subtree of a node contains only nodes with keys greater than the node’s key.
- There must be no duplicate nodes.
Adelson-Velsky and Landis (AVL) Tree
A self-balancing binary search tree where the height of the two child subtrees of any node differ by no more than one. If at any time the heights differ more than one, rebalancing is done to restore this property. AVL trees are optimized for lookup-intensive applications, where frequent insertions and deletions necessitate quick rebalancing to maintain efficient search times.
Balance factor
The balance factor helps in determining the type of rotation needed to maintain the tree’s balance. It must always be -1, 0, or +1.
Balance factor (node) = height(right subtree) - height(left tree)
Rebalance AVL tree
When a node is added/deleted to/from an AVL tree, performing rotations is needed to ensure that the balance factor of all nodes remains within the allowed range.
Tree Traversal
Depth First Search (DFS)
DFS explores as far as possible along each branch before backtracking. Implemented using a stack, either through the system’s call stack via recursion or an explicit stack data structure.
- Used in solving puzzles with only one solution, like mazes.
- Employed in topological sorting, scheduling problems, cycle detection in environments where pathways to vertices need exploration.
Preorder
Preorder traversal visits the root first, followed by the left subtree, and then the right subtree. Captures the root node early, which is helpful for operations that need to replicate or examine the tree structure itself.
- Used to create a copy of the tree.
- Useful in syntax tree applications, such as in compilers and expression parsers, where the structure of the tree aligns with the order of operations.
Inorder
Inorder traversal first visits the left subtree, then the root, and finally the right subtree.
- Commonly used in binary search trees where an ordered list of elements is required.
- Useful in algorithms that need to process nodes in a specific order relative to their hierarchical levels.
Postorder
Postorder traversal visits the left subtree, the right subtree, and the root last. Ideal for situations where operations on a node require results from its children first.
- Commonly used in the calculation of a value for a tree where nodes represent operations in postfix expression evaluation.
- Useful in deleting or freeing nodes and space of the tree in a safe manner.
Breadth First Search (BFS)
BFS explores the neighbor nodes at the present depth prior to moving on to nodes at the next depth level.Implemented using a queue to bring the earliest visited nodes for processing first.
- Used to find the shortest path from a source node to other nodes in an unweighted graph.
- Useful in any searching algorithm where the shortest path is desired, and all edges are of equal weight.
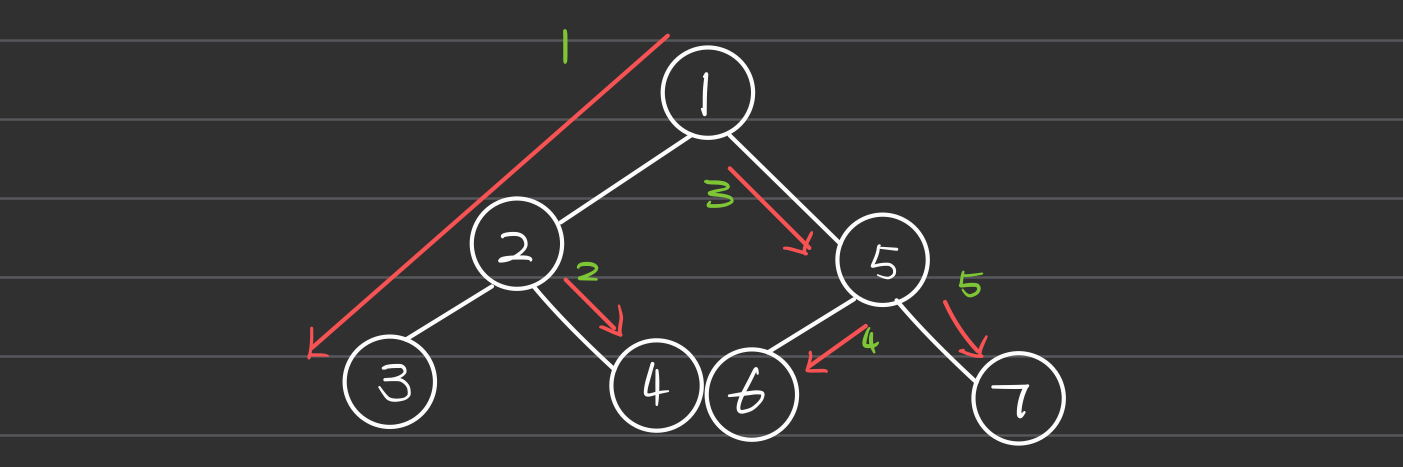
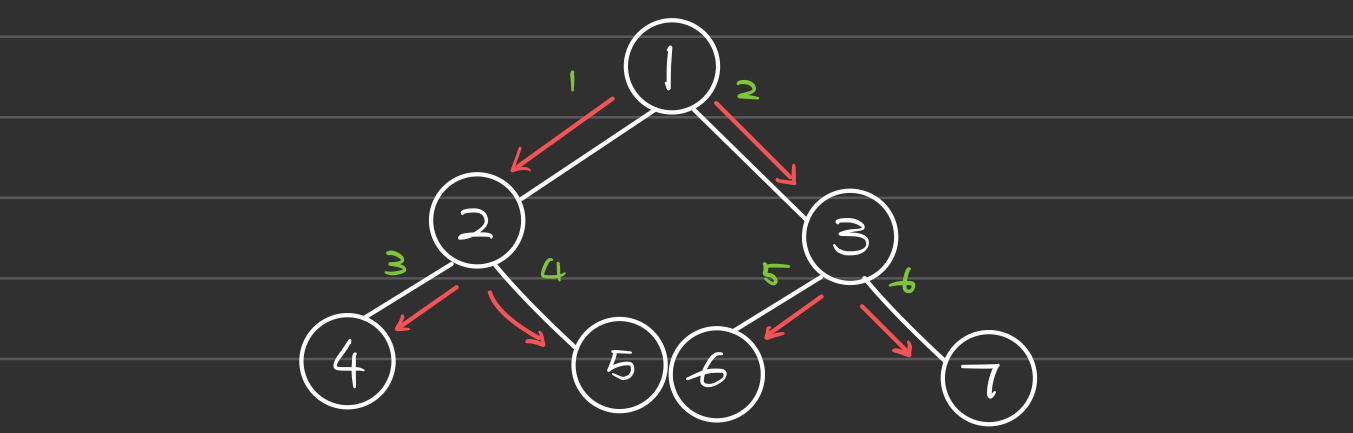
Level Order
Level order traversal visits nodes level by level from top to bottom. This is the same as Breadth-First Search (BFS) for trees.
- Widely used in breadth-first search operations in trees and graphs, such as in finding the shortest path in unweighted graphs.
- Useful in serialization of a tree structure in a way that reconstruction is feasible.